
����Ŀ��Ҫ����28�׳�����ʺ�һ���������ó�Ϊ12��ǽΧ��һ����ͼ1��һ�߿�ǽ�ľ�������������Χ���Ĺ������������������⣬�����æ�������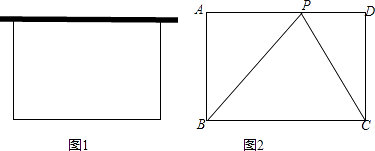
��1���������������Ҫ�����������������������εij������
��2���ڣ�1����ǰ�������£�Ҫ��ǽ��ѡһ����P���ò������������ӷֱ�����BP��CP����Pȡ�ںδ��������ӳ���̣�
��3����Ȼ�Ǿ��������������������£����ѣ�2���еIJ������������Ӹ�Ϊ�����������е��Ե����ӣ���P������ǽ�����ɻ�������sin��BPC�����ֵ��
���𰸡�
��1��
�⣺��������εij�Ϊx�ף�0��x��12�������Ϊ ![]() �ף�
�ף�
���ݾ��ε������ʽ��֪S=x ![]() =��
=�� ![]() ��x��14��2+98��
��x��14��2+98��
��0��x��12���ڴ����������S���ڳ�x�ĺ�������������
�൱x=12ʱ��Sȡ���ֵ��S���=96��
��ʱ ![]() =8��
=8��
�ʰ�����ǽ�ڶ������������γ�Ϊ12�ף���Ϊ2��ʱ������������������
��2��
�⣺����C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����ͼһ��ʾ��
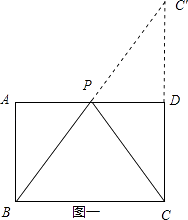
�ߵ�C��C�����AD�Գƣ�
��PC=PC�䣬
��PB+PC=PB+PC��
��������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С��
��AD��BC��
���C��PD�ס�C��BC��
�� ![]() =
= ![]() ��
��
��PD= ![]() BC����PΪAD���е㣮
BC����PΪAD���е㣮
��ʱC��B= ![]() =20���ף���
=20���ף���
�ʵ���Pѡ��AD�е㴦ʱ����Ҫ��������̣��������Ϊ20��
��3��
�⣺��һ��Բ��ʹ��Բ����B��C���Һ�AD���У���ͼ����ʾ��
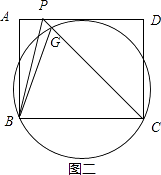
��ȡ�߶�AD��һ��P������BP��CP����CP��Բ���ڵ�G������BG��
�ߡ�BGC=��BPC+��PBG��
���BPC�ܡ�BGC��
��P��G�����غ�ʱȡ�Ⱥţ���ʱ��PΪAD���е㣮
��AD=12��AB=8��
��AP=6��
�ɹ��ɶ����ã�BP= ![]() =10��
=10��
�ߡ�PBC�����S= ![]() BPCPsin��BPC=
BPCPsin��BPC= ![]() ��10��10sin��BPC=
��10��10sin��BPC= ![]() BCAB=
BCAB= ![]() ��12��8��
��12��8��
��sin��BPC= ![]() ��
��
��sin��BPC�����ֵΪ ![]()
����������1����������εij�Ϊx�ף�0��x��12�������Ϊ ![]() �ף����ݾ��ε����=�����������ɵó����S���ڳ�x֮��ĺ�����ϵʽ���ɶ��κ�����x��ȡֵ��Χ�ڵĵ����Լ��ɵó����ۣ���2������C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С���������������ε����ʼ��ɵó�P����AD�е�ʱ���õ�������̣������ʱC��B�ij��ȼ��ɣ���3����һ��Բ��ʹ��Բ����B��C���Һ�AD���У������֪ʶ��Բ�ܽǶ�����֪��BPC�ܡ�BGC��P��G�غ�ʱȡ�Ⱥţ������������ε������ʽ�������ȡ���ֵʱsin��BPC��ֵ��
�ף����ݾ��ε����=�����������ɵó����S���ڳ�x֮��ĺ�����ϵʽ���ɶ��κ�����x��ȡֵ��Χ�ڵĵ����Լ��ɵó����ۣ���2������C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С���������������ε����ʼ��ɵó�P����AD�е�ʱ���õ�������̣������ʱC��B�ij��ȼ��ɣ���3����һ��Բ��ʹ��Բ����B��C���Һ�AD���У������֪ʶ��Բ�ܽǶ�����֪��BPC�ܡ�BGC��P��G�غ�ʱȡ�Ⱥţ������������ε������ʽ�������ȡ���ֵʱsin��BPC��ֵ��
�����㾫����������Ĺؼ�����������Գ�-���·����������֪ʶ��������֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺����1��2014��|�� ![]() |+
|+ ![]() ����
���� ![]() ����0��
����0��
��2���Ȼ�������ֵ����2x��1��2��2��3��2x��������x=��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�տ����������һ���Ϊ����ABCD��С�ݣ�AB+BC=10m.˩סС����10m��������һ�˹̶���B�㴦��С���ڲ��ܽ���С���ڵ������»������Ի���������ΪS��m2��.
����ͼ1����BC��4m����S��m.
����ͼ2���ֿ�����(1)�еľ���ABCDС�ݵ��Ҳ���CDΪ����չһ����CDE����ʹ֮������Ϊ�����ABCED��С�ݣ�������������.����BC�ı仯�����У���Sȡ����Сֵʱ����BC�ij�Ϊm.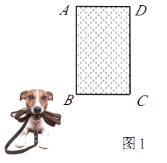
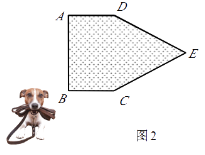
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ֱ���ij�ͺ��ܲ�����ʵ��ͼ��ʾ��ͼ����֪̤��CD��Ϊ2�ף�֧��AC��Ϊ0.8�ף�CD�����ļн�Ϊ12�㣬��ACD=80�㣬��AB��ED�������ֱ���һ��A��صĸ߶�h������ȷ��0.1�ף��ο����ݣ�sin12��=cos78���0.21��sin68��=cos22���0.93��tan68���2.48�� 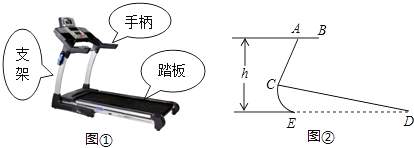
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ����A=60�㣬����C����O�����ߣ�������BO�ڵ�E�� 
��1�����BCE�Ķ�����
��2������O�뾶Ϊ3����BE����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��2016��6�·ݵ��������У������������������������ڵ��������������ĺͲ�������(�� ��)

A. 27 B. 51 C. 69 D. 72
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵxOy�У���A��x�Ḻ�����ϣ���B��y���������ϣ�OA=OB������y=�� ![]() ��ͼ�����߶�AB����M�㣬��AM=BM��
��ͼ�����߶�AB����M�㣬��AM=BM�� 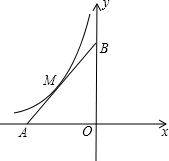
��1�����M�����ꣻ
��2����ֱ��AB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶(1)��ͬѧ����ѧ���,���ýdz�ƽ��һ����(��ͼ).��������·���:
(��)��AOB��һ�������,���dzߵ�ֱ�Ƕ���P��������OA,OB֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M,N�غ�,��PM=PN,���dz߶���P������OP���ǡ�AOB��ƽ����.
(��)��AOB��һ�������,�ڱ�OA,OB�Ϸֱ�ȡOM=ON,���dzߵ�ֱ�Ƕ���P��������OA,OB֮��,�ƶ��dz�ʹ�dz�������ͬ�Ŀ̶���M,N�غ�,��PM=PN,���dz߶���P������OP���ǡ�AOB��ƽ����.
(1)����(��)������(��)�Ƿ����?������,��֤��;��������,��˵������.
(2)�ڷ���(��)PM=PN�������,�����ƶ��dz�,ͬʱʹPM��OA,PN��OB.�˷����Ƿ����?��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��ȫ���ܵ�ȫ���Ĺ㷺��ע��ij��ѧ�Բ���ѧ����У��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ������������в�������ͳ��ͼ����ͼ��ʾ�������ͳ��ͼ�����ṩ����Ϣ����������⣺ 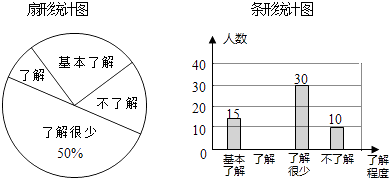
��1�������ʾ������ѧ�������ˣ�����ͳ��ͼ�С������˽⡱��������Ӧ���ε�Բ�Ľ�Ϊ��
��2���벹ȫ����ͳ��ͼ��
��3�����Ӷ�У��ȫ֪ʶ�ﵽ�ˡ��˽⡱�̶ȵ�3��Ů����2�������������ȡ2�˲μ�У��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com