
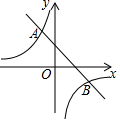
 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).分析 (1)利用待定系数法即可解决问题;
(2)分三种情形讨论①当PA=PB时,可得(n+1)2+4=(n-2)2+1.②当AP=AB时,可得22+(n+1)2=(3$\sqrt{2}$)2.③当BP=BA时,可得12+(n-2)2=(3$\sqrt{2}$)2.分别解方程即可解决问题;
解答 解:(1)把A(-1,2)代入y=$\frac{{k}_{2}}{x}$,得到k2=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$.
∵B(m,-1)在Y=-$\frac{2}{x}$上,
∴m=2,
由题意$\left\{\begin{array}{l}{-{k}_{1}+b=2}\\{2{k}_{1}+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为y=-x+1.
(2)∵A(-1,2),B(2,-1),
∴AB=3$\sqrt{2}$,
①当PA=PB时,(n+1)2+4=(n-2)2+1,
∴n=0,
∵n>0,
∴n=0不合题意舍弃.
②当AP=AB时,22+(n+1)2=(3$\sqrt{2}$)2,
∵n>0,
∴n=-1+$\sqrt{14}$.
③当BP=BA时,12+(n-2)2=(3$\sqrt{2}$)2,
∵n>0,
∴n=2+$\sqrt{17}$.
综上所述,n=-1+$\sqrt{14}$或2+$\sqrt{17}$.
点评 本题考查反比例函数综合题.一次函数的性质、待定系数法、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用 分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
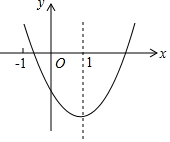 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:| A. | ①④ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
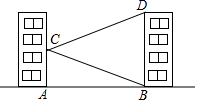 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
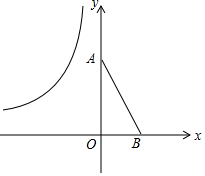 如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$).
如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com