
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据计算CD的长为22cm(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 分析 作DM⊥AB于M,在Rt△BCN中,由三角函数求出BC≈83.3(cm),BN≈66.7(cm),求出AN的长,证出△ADM是等腰直角三角形,得出AM=DM=50cm,即可得出CD的长.
解答 解:作DM⊥AB于M,如图所示: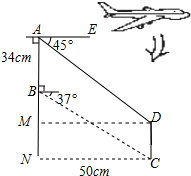 在Rt△BCN中,BC=CN÷cos37°=50÷0.8=62.5(cm),
在Rt△BCN中,BC=CN÷cos37°=50÷0.8=62.5(cm),
∴BN=BC•sin37°=62.5×0.80≈37.5(cm),
∴AN=AB+BN=34+37.5=71.5cm,
∵∠DAE=45°,∠BAE=90°,
∴∠DAM=45°,
∴△ADM是等腰直角三角形,
∴AM=DM=50cm,
∴CD=MN=AN-AM=71.5-50≈22(cm);
故答案为:22.
点评 本题考查了解直角三角形的应用、三角函数、等腰直角三角形的判定与性质;熟练掌握解直角三角形的方法,求出BN是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{361}{x-145}$-$\frac{361}{x}$=1.4 | B. | $\frac{361}{x}$-$\frac{361}{x-145}$=1.4 | ||
| C. | $\frac{361}{x}$-$\frac{361}{x+145}$=1.4 | D. | x+1.4(x+145)=361 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
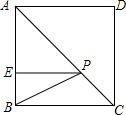 如图,正方形ABCD的边长为5,E是AB上一点,且BE:AE=1:4,若P是对角线AC上一动点,则PB+PE的最小值是$\sqrt{41}$.(结果保留根号)
如图,正方形ABCD的边长为5,E是AB上一点,且BE:AE=1:4,若P是对角线AC上一动点,则PB+PE的最小值是$\sqrt{41}$.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2+3-5-4-3 | B. | -2+3+5-4+3 | C. | -2+3+5+4-3 | D. | -2+3+5-4-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | -1 | C. | 1±$\sqrt{2}$ | D. | 1$±\sqrt{2}$或-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com