M.N是线段AB的垂直平分线上的两点.且∠NBA=15°,∠MBA=45°．先画出图形.再求∠MAN的度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

M、N是线段AB的垂直平分线上的两点，且∠NBA=15°；∠MBA=45°．先画出图形，再求∠MAN的度数．

答案：略
解析：

30°或60°

练习册系列答案

大联考期末复习合订本系列答案

新题型全能测评课课练天津科学技术出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

51、如图所示，直线AB，CD相交于点O，P是CD上一点．
（1）过点P画AB的垂线段PE．
（2）过点P画CD的垂线，与AB相交于F点．
（3）说明线段PE，PO，FO三者的大小关系，其依据是什么？

查看答案和解析>>

科目：初中数学 来源： 题型：

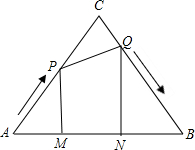如图，等边三角形ABC的边长为8cm，动点P从点A出发以2cm/秒的速度沿AC方向向终点C运动，同时动点Q从点C出发以1cm/秒的速度沿CB方向向终点B运动，过点P、Q分别作边AB的垂线段PM、QN，垂足分别为点M、N．
设P、Q两点运动时间为t秒（0＜t＜4），四边形MNQP的面积为Scm²．
（1）当点P、Q在运动的过程中，t为何值时，△PCQ是直角三角形？
（2）求四边形MNQP的面积S随运动时间t变化的函数关系式．
（3）是否存在某一时刻t，使四边形MNQP的面积S等于△ABC的面积的

？若存在，求出此时t的值；若不存在，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

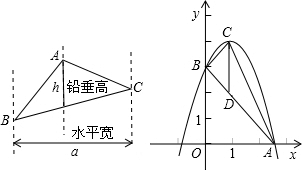
7、如图，BD是等腰△ABC（顶角∠A是锐角）腰AC上的高，在△ABC内作一只45°的角∠EBC交AC于点E，过E作AB的垂线段EF，垂足为F．则线段DE与线段EF的大小关系为（　　）

A、DE＞EF

B、DE=EF

C、DE＜EF

D、与∠A的大小有关，无法判断

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

（2013•丰南区一模）阅读材料：如图，过△ABC的三个顶点分别作出水平垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”（a），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（h）”．我们可以得出一种计算三角形面积的新方法：S_△ABC=

ah，即三角形面积等于水平宽与铅垂高乘积的一半．
解答下列问题：如图，抛物线顶点坐标为点C（1，4）交x轴于点A，交y轴于点B（0，3）

（1）求抛物线解析式和线段AB的长度；
（2）点P是抛物线（在第一象限内）上的一个动点，连接PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及S_△CAB；
（3）在第一象限内抛物线上求一点P，使S_△PAB=S_△CAB．

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

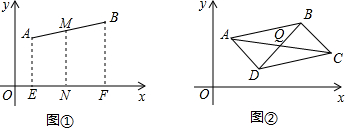让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是

．再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x₁，y₁），B（x₂，y₂），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（

x1+x2

，

y1+y2

）（用x₁，y₁，x₂，y₂表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x₁，y₁），B（x₂，y₂），C（x₃，y₃），D（x₄，y₄），则其对角线交点Q的坐标可以表示为Q（

x1+x3

，

y1+y3

），也可以表示为Q（

x2+x4

，

y2+y4

），经过比较，我们可以分别得出关于x₁，x₂，x₃，x₄及，y₁，y₂，y₃，y₄的两个等式是

x₁+x₃=x₂+x₄

和

y₁+y₃=y₂+y₄

．我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的

和相等

．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学