
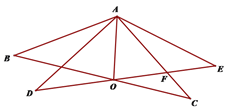
【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .
【答案】(1)证明见解析;(2)证明见解析;(3)40°或20°
【解析】试题分析:(1)根据全等三角形的判定“SAS”证得△ABC≌△ADE,然后根据全等的性质,可得∠B=∠D,再根据三角形的内角和定理得证结论;
(2)过A作AM⊥BC于M,作AN⊥DE于N,由(1)知△ABC≌△ADE,根据全等三角形的面积相等,证得AM=AN,从而AO为∠DAC的平分线,根据ASA证得△ABO≌△AEO,可得AB=AE,然后得证;
(3)由题意可分为OA=OF和OA=AF两种情况讨论,即可求解.
试题解析:(1)在△ABC和△ADE中,
∵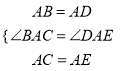
∴△ABC≌△ADE(SAS)∴∠B=∠D,∴∠BOD=∠BAD=α,
(2)过A作AM⊥BC于M,作AN⊥DE于N,
∵△ABC≌△ADE,∴S△ABC=S△ADE,∴![]() ,∵BC=DE,∴AM=AN,
,∵BC=DE,∴AM=AN,
∴AO平分∠BOE,∵AO平分∠DAC,∴∠DAO=∠CAO,∴∠BAO=∠EAO,
在△ABO和△AEO中,
∵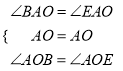
∴△ABO≌△AEO(ASA),
∴AB=AE,∵AB=AD,AC=AE,∴AC=AD,
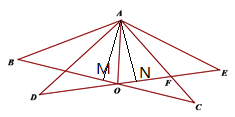
(3)当AO=AF时,a=40°,
当OA=OF时,a=20°,
故答案为:40°或20°.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx与x轴交于O,A(4,0)两点,点B的坐标为(0,-3).
(1)求抛物线的对称轴;
(2)已知点P在抛物线的对称轴上,连接OP,BP. 若要使OP+BP的值最小,求出点P的坐标;
(3)将抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象. 当直线y=x+m(m≠0)与这个新图象有两个公共点时,在反比例函数y=![]() 的图象中,y的值随x怎样变化?判断并说明理由.
的图象中,y的值随x怎样变化?判断并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com