
【题目】在平面直角坐标系中,横、纵坐标都为整数的点称为整点.如图,从内向外依次为第![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 个正方形(实线),若整点
个正方形(实线),若整点![]() 在第
在第![]() 个正方形的边上,则
个正方形的边上,则![]() ,
,![]() ,
,![]() 之间满足的数量关系为_______.
之间满足的数量关系为_______.

【答案】![]()
【解析】
解这道题时,先分别探究第1个正方形上的4个整点的坐标,第2个正方形上的8个整点的坐标,第3个正方形上的12个整点的坐标彼此之间的关系,进而可总结得到n与a和b之间的规律,问题自然解决.
解:由图可知,第1个正方形四条边上的格点共有4个,
它们的坐标分别为:(1,0),(0,1),(﹣1,0),(0,﹣1),
且这4个点的横纵坐标的绝对值之和为1;
第2个正方形四条边上的格点共有8个,
它们的坐标分别为:(2,0),(1,1),(0,2),(﹣1,1),(﹣2,0),(﹣1,﹣1),(0,﹣2),(1,﹣1),
且这8个点的横纵坐标的绝对值之和为2;
第3个正方形四条边上的格点共有12个,
它们的坐标分别为:(3,0),(2,1),(1,2),(0,3),(﹣1,2),(﹣2,1),(﹣3,0),(﹣2,﹣1),(﹣1,﹣2),(0,﹣3),(1,﹣2),(2,﹣1),
且这12个点的横纵坐标的绝对值之和为3;
由此可知:若整点![]() 在第
在第![]() 个正方形的边上,则
个正方形的边上,则![]() ,
,![]() ,
,![]() 之间满足的数量关系为
之间满足的数量关系为![]() ,
,
故答案为:![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )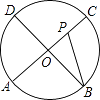
A.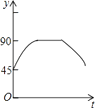
B.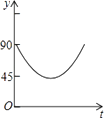
C.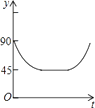
D.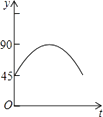
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.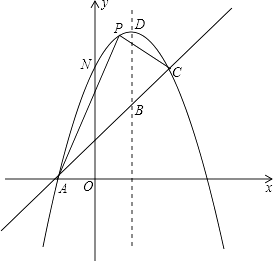
(1)抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F. 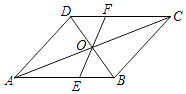
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
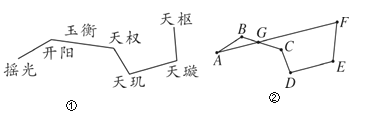
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强爱国主义教育,提高思想道德素质,某中学决定组织部分班级去山西国民师范旧址革命活动纪念馆开展红色旅游活动,在参加此次活动的师生中,若每位教师带17名学生,还剩12名学生没人带;若每位教师带18名学生,就有一位教师少带4名学生.现有甲、乙两种大客车,两种客车的载客量和租金如下表所示.
类别 | 甲种客车 | 乙种客车 |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 420 |
(1)参加此次红色旅游活动的教师和学生各有多少人?
(2)为了安全,每辆客车上要有2名教师.则怎样租车可以保证师生均有车坐,而且每辆车上都没有空座,也不超载,此时租车的费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com