
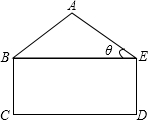
 某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=
某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=| 3 | 4 |
| FE |
| AF |
| 3 |
| 4 |
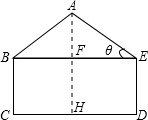 解:作AH⊥CD,垂足为H,交EB于点F,由矩形BCDE,得AH⊥BE.
解:作AH⊥CD,垂足为H,交EB于点F,由矩形BCDE,得AH⊥BE.| 3 |
| 4 |
| AF |
| EF |
| 3 |
| 4 |
| 15 |
| 34 |
| 15 |
| 34 |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
 某工厂接受一批支援四川省汶川灾区抗震救灾账篷的生产任务.根据要求,账篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰三角形ABE的底角∠AEB=θ,且tanθ=
某工厂接受一批支援四川省汶川灾区抗震救灾账篷的生产任务.根据要求,账篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰三角形ABE的底角∠AEB=θ,且tanθ=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(江苏盐城卷)数学(带解析) 题型:解答题
某工厂接受一批支援四川省汶川灾区抗震救灾帐蓬的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ= ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(江苏盐城卷)数学(解析版) 题型:解答题
某工厂接受一批支援四川省汶川灾区抗震救灾帐蓬的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ= ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源:2008年广东省深圳市实验中学高一直升考试数学试卷(解析版) 题型:解答题
 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m,求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)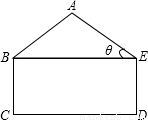
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com