
����Ŀ���п��ٽ���ij�̼�ץס�̻�������һ������ר�ñʼ��ľߴ���ȥ�����·ݣ��ʵ��ۼ۱��ľߴ����ۼ���2Ԫ���ʺ��ľߴ�����������Ϊ100����������ľߴ��������۶�Ϊ1400Ԫ��
��1����ȥ�����·ݱʺ��ľߴ����ۼۣ�
��2�����г�Ӱ�죬���̼ҹ��ƽ������·ݹ���ʵ��˻���٣����ǽ����˱ʵ��ۼۣ�����������·ݱʵ�����������������ͳ�Ʒ�����ȥ�����·�����ľߴ����ۼ�ÿ����1Ԫ���ľߴ���������������10����ͬʱ�ʵ�������������20�����ұʵ��ۼ۲��䣮����������·ݱʺ��ľߺе������۶��ȥ�����·ݵıʺ��ľߺе������۶��90Ԫ����������·��ľߴ����ۼۣ�
���𰸡���1��ȥ�����·ݱʵ��ۼ�Ϊ6Ԫ���ľߴ����ۼ�Ϊ8Ԫ����2���������·��ľߴ����ۼ�Ϊ7Ԫ��
��������
��1����ȥ�����·ݱʵ��ۼ�ΪxԪ���ľߴ����ۼ�ΪyԪ�����ݱʵ��ۼ۱��ľߴ����ۼ���2Ԫ������۱ʺ��ľߴ���100�������۶�Ϊ1400Ԫ�����ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2����������·��ľߴ����ۼ�ΪmԪ�����ľߴ���������Ϊ[100+10��8��m��]�����ʵ�������Ϊ[100+20��8��m��]���������ܼۣ����������������ɵó�����m��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
��1����ȥ�����·ݱʵ��ۼ�ΪxԪ���ľߴ����ۼ�ΪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��ȥ�����·ݱʵ��ۼ�Ϊ6Ԫ���ľߴ����ۼ�Ϊ8Ԫ��
��2����������·��ľߴ����ۼ�ΪmԪ�����ľߴ���������Ϊ[100+10��8��m��]�����ʵ�������Ϊ[100+20��8��m��]����
�����⣬�ã�m[100+10��8��m��]+6[100+20��8��m��]��1400+90��
�������ã�m2��6m��7��0��
��ã�m1����1��m2��7��
�𣺽������·��ľߴ����ۼ�Ϊ7Ԫ��


 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ࡱ��ʶ���������ģ���ͼ�������е��ĸ���ͬ����������Ͷ��Ͱ���ֱ�д�ţ��к����������������������������ɻ�������������С��Ͷ����һ��������С��Ͷ��������������
��1��ֱ��д��С��Ͷ�ŵ�����ǡ���ǡ������������ĸ��ʣ�
��2����С��Ͷ�ŵ�����������ͬ��ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ˮ���ӵĺ����Ϊ�ı���ABCD������AD��BC���Ӷ�BC=10�ף��Ӹ�20�ף�б��AB���¶�i=1��2.5��б��CD���½�Ϊ30�㣮
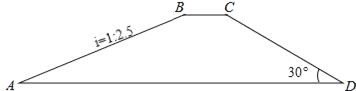
��1����ӵ�AD�ij��ȣ������ȷ��1�ף���
��2�����ӳ�100�ף�������������Ҫ����ʯ�ϣ��ο����ݣ� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
��![]() �������30ǧ�ף���֪�ס������˷ֱ������г���Ħ�г���
�������30ǧ�ף���֪�ס������˷ֱ������г���Ħ�г���![]() �س���ǰ��
�س���ǰ��![]() �أ�;��������������Щʱ�䣬Ȼ���ּ�����·.ͼ5�е��߶�
�أ�;��������������Щʱ�䣬Ȼ���ּ�����·.ͼ5�е��߶�![]() ������
������![]() �ֱ�ӳ�˼ס����������е�·��
�ֱ�ӳ�˼ס����������е�·��![]() ��ǧ�ף���ʱ��
��ǧ�ף���ʱ��![]() ���֣��ĺ�����ϵ������ͼ���ṩ����Ϣ�ش��������⣺
���֣��ĺ�����ϵ������ͼ���ṩ����Ϣ�ش��������⣺
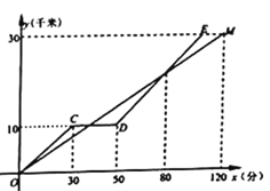
��1���������г����ٶ���_________ǧ��/���ӣ�
��2�����˵ڶ�������ʱ����![]() ��________ǧ�ף�
��________ǧ�ף�
��3���߶�![]() ��ӳ�����ó������е�·��
��ӳ�����ó������е�·��![]() ��ǧ�ף���ʱ��
��ǧ�ף���ʱ��![]() ���֣��ĺ�����ϵ.������߶�
���֣��ĺ�����ϵ.������߶�![]() �ı���ʽ���䶨����.
�ı���ʽ���䶨����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
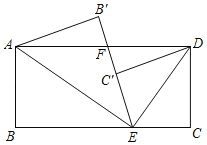
����Ŀ����ͼ��ʾ���ھ���ABCD�У�AB��1�����߶�BC��ȡһ��E������AE��ED������ABE��AE���ۣ�ʹ��B����B'�����߶�EB'��AD�ڵ�F������ECD��DE���ۣ�ʹ��C�Ķ�Ӧ��C'�����߶�EB'�ϣ��ҵ�C'ǡ��ΪEB'���е㣬���߶�EF�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������ڹ�ԭ���һ��ֱ�߶Գƣ�����������ǻ�Ϊ����㣬����ֱ�߽о���ֱ�ߣ���A��2��3����B��3��2������y��xΪ����ֱ�ߵľ���㣮
��1��M��4��1����N����1����4����һ�Ծ���㣬����ֱ��Ϊ_____��
��2����y��![]() xΪ����ֱ�ߣ�E����2��0���ľ����Ϊ_____��
xΪ����ֱ�ߣ�E����2��0���ľ����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ8��������OABC���������������ϣ��Ե�CΪ����������߾�����A����P���������ϵ�A��C���һ�����㣨���˵㣩������P��PF��BC�ڵ�F����D��E������ֱ�Ϊ��0��6��������4��0��������PD��PE��DE��
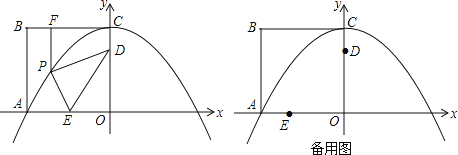
��1���������ߵĽ���ʽ��
��2����d��|PD��PF|����˵��d�Ƿ�Ϊ��ֵ�����Ƕ�ֵ����������С�������Ƕ�ֵ����˵����仯���ɣ�
��3�������PDE�ܳ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��20Ԫ���ۼ�Ϊÿ��30Ԫ��ÿ���¿�����180�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ���¾ͻ�������10������ÿ���ۼ۲��ܸ���35Ԫ����ÿ����Ʒ���ۼ�����xԪ��xΪ��������ÿ���µ���������ΪyԪ��
��1����y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ����xΪ��ֵʱy��ֵΪ1920��
��2��ÿ����Ʒ���ۼ�Ϊ����Ԫʱ��ÿ���¿ɻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�
��![]() ��
��![]() (
(![]() )����
)����![]() Ϊֱ����Բ��
Ϊֱ����Բ��![]() ����
����![]() ��
Ϊ��![]() ��һ���㣮
��һ���㣮
��1���ж�����ԭ��![]() �Ƿ��ڡ�
�Ƿ��ڡ�![]() �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ�
��2������![]() �ڵ�һ���ޣ�����
�ڵ�һ���ޣ�����![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ������
������![]() ����
����![]() ����
����![]() ʱ�����߶�
ʱ�����߶�![]() �ij�:
�ij�:
��3������![]() ��
��![]() ���е㣬��������
���е㣬��������![]() �ı仯��
�ı仯��![]() �������Ƿ����仯�������䣬�����
�������Ƿ����仯�������䣬�����![]() �����ꣻ���仯����˵�����ɣ�
�����ꣻ���仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com