
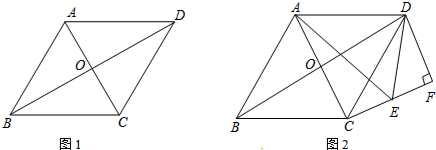
分析 (1)①依题意补全图形如图1所示;
②由菱形的性质得到AE=CE,然后用勾股定理得到CE2=EF2+CF2,代换即可;
(2)作辅助线,得到DE=DG,∠EDG=2∠EDF,再由旋转和菱形的性质得到∠ADE=∠CDG,判断出△ADE≌△CDG,即AE=CG,最后代换即可.
解答 解(1)①依题意补全图形如图1所示,
②连接CE,
∵四边形ABCD为菱形,
∴BD⊥AC,BD平分AC,
∴AE=CE,
∵EF⊥CD,
∴∠EFC=90°,
根据勾股定理得,CE2=EF2+CF2,
∴AE2=EF2+CF2,
故答案为AE2=EF2+CF2;
(2)如图2,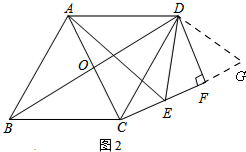
延长EF至G,使EF=FG,连接DG,
∴EG=2EF,
∵DF⊥CF,
∴DE=DG,∠EDG=2∠EDF
∵四边形ABCD是菱形,
∴AD=CD,∠ADC=2∠0DC=60°,
由旋转得,∠ODC=∠EDF,
∴∠ADC=∠EDG,
∴∠ADE=∠CDG,
在△ADE和△CDG中
∵$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDG}\\{DE=DG}\end{array}\right.$,
∴△ADE≌△CDG,
∴AE=CG=CE+EG=CE+2EF,
∴AE=CE+2EF,
故答案为AE=CE+2EF.
点评 此题是四边形综合题,主要考查了菱形的性质,旋转的性质,勾股定理的运用,全等三角形的判定,解本题的关键是作出辅助线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
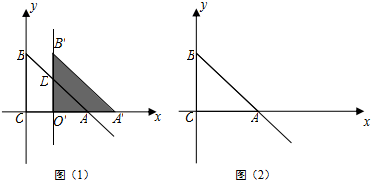
 如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)
如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”.
P是⊙O内一点,过点P作⊙O的任意一条弦AB,我们把PA•PB的值称为点P关于⊙O的“幂值”. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com