
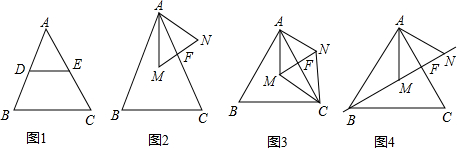
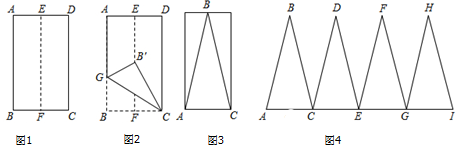
分析 (1)根据两个图形必须是相似形得到∠ADE=∠B,根据平行线的性质证明即可;
(2)①延长AM交BC于D,根据等腰三角形三线合一得到∠DAC=30°,求出∠AFM=90°,得到答案;②由四边形AMCN为菱形,得到AC平分∠MAN,∠MAC=30°,于是得到∠BAM=30°,根据四边形AMCN为菱形,得到AF=$\frac{1}{2}$AC,AC⊥MN,解直角三角形得到AF=$\frac{\sqrt{3}}{2}$AM,$\frac{\sqrt{3}}{2}$AM=$\frac{1}{2}$AC,AC=$\sqrt{3}$AM,由于△ABC为等边三角形,得到AC=AB,求得AB=$\sqrt{3}$AM根据相似三角形的性质得到$\frac{AM}{AB}=\frac{k}{1}$,即可得到结论;③如图4,过A作AH⊥MN于H,由于△AMN是等边三角形,同时代的AH=AM•cos30°=$\frac{\sqrt{3}}{2}$AM,根据三角函数的定义即可得到结论.
解答 (1)证明:∵△ADE是△ABC的位似图形,
∴△ADE∽△ABC,
∴∠ADE=∠B,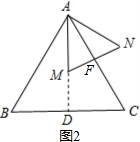
∴DE∥BC;
(2)①AC⊥MN,
证明:如图2,延长AM交BC于D,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠DAC=30°,又∠AMN=60°,
∴∠AFM=90°,即AC⊥MN;
②∵四边形AMCN为菱形,
∴AC平分∠MAN,∠MAC=30°,
∴∠BAM=30°,
∴α=30°,
∵四边形AMCN为菱形,
∴AF=$\frac{1}{2}$AC,AC⊥MN,
在Rt△△AFM中,cos30°=$\frac{AF}{AM}$,
∴AF=$\frac{\sqrt{3}}{2}$AM,
∴$\frac{\sqrt{3}}{2}$AM=$\frac{1}{2}$AC,AC=$\sqrt{3}$AM,
∵△ABC为等边三角形,
∴AC=AB,
∴AB=$\sqrt{3}$AM,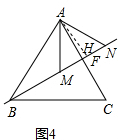
∵△ADE是△ABC的位似图形,位似比为k:1,
∴△AMN∽△ABC,位似比为k:1,$\frac{AM}{AB}=\frac{k}{1}$,AM=kAB,
∴k=$\frac{\sqrt{3}}{3}$,
③如图4,过A作AH⊥MN于H,
∵△AMN是等边三角形,
∴AH=AM•cos30°=$\frac{\sqrt{3}}{2}$AM,
在Rt△AHB中,∠BAH=α+30°,
∴cos∠BAH=cos(α+30°)=$\frac{AH}{AB}$,
∴AH=AB•cos(α+30°),AB•cos(α+30°)=$\frac{\sqrt{3}}{2}$AM,
由②得:AM=kAB,
∴cos(α+30°)=$\frac{\sqrt{3}}{2}$k.
点评 本题考查的是位似变换的性质、旋转变换以及等边三角形的性质,掌握两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
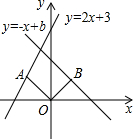 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各边相等的多边形是正多边形 | B. | 同角或等角的余角相等 | ||
| C. | 必然事件发生的概率为0 | D. | 六边形的内角和等于540° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
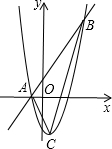 如图,抛物线y=a(x-1)2-n与直线y=2x+b相交于点A(-1,0)和点B(m,12).
如图,抛物线y=a(x-1)2-n与直线y=2x+b相交于点A(-1,0)和点B(m,12).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.22×104亿 | B. | 0.622×105亿 | C. | 6.22×105亿 | D. | 62.2×103亿 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2×1010 | B. | 2×109 | C. | 20×108 | D. | 2×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com