
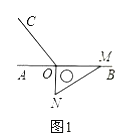
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作射线
点作射线![]() ,使
,使![]() ,将一直角三角板的直角项点放在点
,将一直角三角板的直角项点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
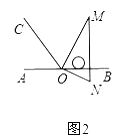
![]() 如图2,将图1中的三角板绕点
如图2,将图1中的三角板绕点![]() 逆时针旋转,使边
逆时针旋转,使边![]() 在
在![]() 的内部,且
的内部,且![]() 恰好平分
恰好平分![]() .此时
.此时![]() __ 度;
__ 度;
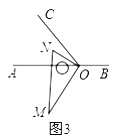
![]() 如图3,继续将图2中的三角板绕点
如图3,继续将图2中的三角板绕点![]() 按逆时针方向旋转,使得
按逆时针方向旋转,使得![]() 在
在![]() 的内部.试探究
的内部.试探究![]() 与
与![]() 之间满足什么等量关系,并说明理由;
之间满足什么等量关系,并说明理由;
![]() 将图1中的三角板绕点
将图1中的三角板绕点![]() 按每秒
按每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,若第
的速度沿逆时针方向旋转一周,在旋转的过程中,若第![]() 秒时,
秒时,![]() 三条射线恰好构成相等的角,则
三条射线恰好构成相等的角,则![]() 的值为__ (直接写出结果).
的值为__ (直接写出结果).
【答案】(1)25°;(2)∠AOM-∠NOC=40°,理由详见解析;(3)t的值为13,34,49或64.
【解析】
(1)由平角的定义先求出∠BOC的度数,然后由角平分线的定义求出∠BOM的度数,再根据∠BON=∠MON-∠BOM可以求出结果;
(2)根据题意得出∠AOM+∠AON=90°①,∠AON+∠NOC=50°②,利用①-②可以得出结果;
(3)根据已知条件可知,在第t秒时,三角板转过的角度为5°t,然后按照OA、OC、ON三条射线构成相等的角分四种情况讨论,即可求出t的值.
解:(1)∵∠AOC=50°,
∴∠BOC=180°-∠AOC=130°,
∵OM平分∠BOC,∴∠BOM=![]() ∠BOC=55°,
∠BOC=55°,
∴∠BON=90°-∠BOM=25°.
故答案为:25;
(2)∠AOM与∠NOC之间满足等量关系为:∠AOM-∠NOC=40°,
理由如下:∵∠MON=90°,∠AOC=50°,
∴∠AOM+∠AON=90°①,∠AON+∠NOC=50°②,
∴①-②得,∠AOM-∠NOC=40°.
(3)∵三角板绕点O按每秒5°的速度沿逆时针方向旋转,
∴第t秒时,三角板转过的角度为5°t,
当三角板转到如图①所示时,∠AON=∠CON.
∵∠AON=90°+5°t,∠CON=∠BOC+∠BON=130°+90°-5°t=220°-5°t,
∴90°+5°t=220°-5°t,
即t=13;
当三角板转到如图②所示时,∠AOC=∠CON=50°,
∵∠CON=∠BOC-∠BON=130°-(5°t-90°)=220°-5°t,
∴220°-5°t=50°,
即t=34;
当三角板转到如图③所示时,∠AON=∠CON=![]() ∠AOC=25°,
∠AOC=25°,
∵∠CON=∠BON-∠BOC=(5°t-90°)-130°=5°t-220°,
∴5°t-220°=25°,
即t=49;
当三角板转到如图④所示时,∠AON=∠AOC=50°,
∵∠AON=5°t-180°-90°=5°t-270°,
∴5°t-270°=50°,
即t=64.
故t的值为13,34,49或64.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数 | 碟子的高度(单位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年618年中大促活动中,各大电商分期进行降价促销.某宝店铺热销网红A款服装进行价格促销,促销价比平时售价每件降90元,如果卖出相同数量的A款服装,平时销售额为5万元,促销后销售额只有4万元.
(1)该店铺A款服装平时每件售价为多少元?
(2)该店铺在6.1—6.2第一轮促销中,A款服装的销售情况非常火爆,商家决定为第二轮6.16—6.18大促再进一批货,经销A款的同时再购进同品牌的B款服装,己知A款服装每件进价为300元,B款服装每件进价为200元,店铺预计用不少于7.2万元且不多于7.3万元的资金购进这两款服装共300件.请你算一算,商家共有几种进货方案?
(3)在6.16—6.18促销活动中,A款仍以平日价降90元促销,B款服装每件售价为280元,为打开B款服装的销路,店铺决定每售出一件B款服装,返还顾客现金![]() 元,要使(2)中所购进服装全部售完后所有方案获利相同,
元,要使(2)中所购进服装全部售完后所有方案获利相同,![]() 的值应是多少?
的值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
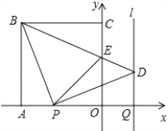
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若△ABC中,其中一个内角是另一个内角的一半,则称△ABC为“半角三角形”.根据此定义,完成下面各题:
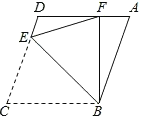
(1)若△ABC为半角三角形,且∠A=90°,则△ABC中其余两个角的度数为 ;
(2)若△ABC是半角三角形,且∠C=40°,则∠B ;
(3)如图,在四边形ABCD中,AB∥CD,AD∥BC,∠C=72°,点E在边CD上,以BE为折痕,将△BCE向上翻折,点C恰好落在AD边上的点F,若BF⊥AD,则△EDF是半角三角形吗?若是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是_____.
m)(m为非负数),则CA+CB的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【本小题满分9分】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
(1)B班参赛作品有多少件?
(2)请你将图②的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
(4)将写有A、B、C、D四个字母的完全相同的卡片放人箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于方程![]() =1,某同学解法如下:
=1,某同学解法如下:
解:方程两边同乘6,得3x﹣2(x﹣1)=1 ①
去括号,得3x﹣2x﹣2=1 ②
合并同类项,得x﹣2=1 ③
解得x=3 ④
∴原方程的解为x=3 ⑤
(1)上述解答过程中的错误步骤有 (填序号);
(2)请写出正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com