
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?

【答案】(1)100,450;(2)小强先到山顶,小强爬了15分钟;(3)图中两条线段的交点表示小强和爷爷相遇的时候,这时小强爬山用时10分钟,离山脚300米.
【解析】
(1)由图可知,爷爷比小强先上了100米,由点(10,300)求出小强的速度30米/分,即可求山高;
(2)根据图象即可得出答案;
(3)图中两条线段的交点表示小强和爷爷相遇的时候,再根据交点的坐标即可得出小强爬山的时间和距离山脚的高度.
解:(1)由图可知,爷爷比小强先上了100米,
当小强爬了10分钟,爬了300米
∴小强的速度300÷10=30米/分,
∴山高30×15=450米;
(2)由图象可知,小强先到山顶,小强爬了15分钟;
(3)图中两条线段的交点表示小强和爷爷相遇的时候,交点为(10,300),由交点坐标可知,这时小强爬山用时10分钟,离山脚300米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
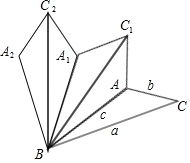
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一段![]() 米长的河堤的整治任务,打算请
米长的河堤的整治任务,打算请![]() 两个工程队来完成,经过调查发现,
两个工程队来完成,经过调查发现,![]() 工程队每天比
工程队每天比![]() 工程队每天多整治
工程队每天多整治![]() 米,
米,![]() 工程队单独整治的工期是
工程队单独整治的工期是![]() 工程队单独整治的工期的
工程队单独整治的工期的![]() .
.
(1)问![]() 工程队每天分别整治多少米?
工程队每天分别整治多少米?
(2)由![]() 两个工程队先后接力完成,共用时
两个工程队先后接力完成,共用时![]() 天,问
天,问![]() 工程队分别整治多少米?
工程队分别整治多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克),获得的总利润为 (元);
(2)设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,连接
,连接![]() ,将
,将![]() 对折,点
对折,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,得折痕
处,得折痕![]() ;将
;将![]() 对折,点
对折,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,得折痕
处,得折痕![]() ,当
,当![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上时.若令
上时.若令![]() 的面积为
的面积为![]() ,
,![]() 的长度为
的长度为![]() ,则
,则![]() 关于
关于![]() 的函数解析式是( )
的函数解析式是( )
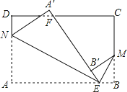
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
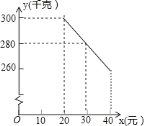
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com