
����Ŀ��С����ѧУ��֯���������и����˽�������ס��С��450������ļ�ͥ������������������������40�������ͥ�������������ȡ��������λ��Ԫ���������������µ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
���� | Ƶ�� | �ٷֱ� |
600��x��800 | 2 | 5% |
800��x��1000 | 6 | 15% |
1000��x��1200 | 45% | |
9 | 22.5% | |
1600��x��1800 | 2 | |
�ϼ� | 40 | 100% |
���������ṩ����Ϣ������������⣺
��1����ȫƵ���ֲ�����
��2����ȫƵ���ֲ�ֱ��ͼ��

��3��������Ƹþ���С����ͥ�����е����루����1000����1600Ԫ���Ĵ�Լ�ж��ٻ���
���𰸡���1������������2������������3��338��
����������1����������ɵó��ֲ��ǣ�1200��x��1400��1400��x��1600��
1000��x��1200�аٷֱ�ռ45%������40��0.45=18�ˣ�
1600��x��1800��������2�ˣ���ռ![]() =0.05���ʰٷֱ�Ϊ5%��
=0.05���ʰٷֱ�Ϊ5%��
��ʣ��1400��x��1600��������3��ռ7.5%��
��2��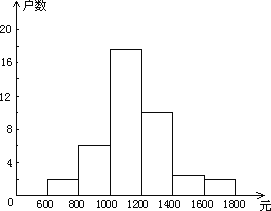
��3������1000������1600��ռ75%����450��0.75=337.5��338����
�𣺾���С����ͥ�����е�����Ĵ�Լ��338����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�ı��Ϊ132Ԫ�����Ա�۵�9�۳��ۣ��Կɻ���10%�������Ʒ�Ľ���Ϊ��������
A.105Ԫ
B.106Ԫ
C.108Ԫ
D.118Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������ABDƽ�ƣ�ʹD��BD�ӳ�������C�õ���A��B��D�䣬A��B�佻AC��E��ADƽ����BAC��
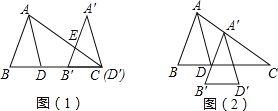
��1��������B��EC����A��֮��Ĺ�ϵ����д�����ɣ�
��2����ͼ����ABDƽ������ͼ��2����ʾ���õ���A��B��D�䣬���ʣ�A��Dƽ����B��A��C��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����5��0����B��3��0����
��1����y������һ��C��ʹ֮����S��ABC=16�����C�����꣨Ҫ�б�Ҫ�IJ��裩��
��2����ֱ������ƽ������һ��C��������S��ABC=16��C�ж��ٸ�����Щ����ʲô������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2+bx+c��y�ύ�ڵ�C����![]() �ύ�ڵ�A��B����AB��2�������ߵ��Գ���Ϊֱ��x=2��
�ύ�ڵ�A��B����AB��2�������ߵ��Գ���Ϊֱ��x=2��
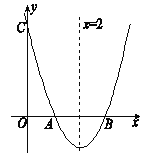
��1�� �������ߵĺ�������ʽ��
��2�� ��������ߵ��Գ���������һ��P��ʹ����APC�ܳ�����С�����ʱ��APC�ܳ���
��3�� ��DΪ��������һ����EΪ�Գ�����һ�������Ե�A��B��D��EΪ������ı��������Σ�����D����������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��2.5�׳�������ABб������ֱ��ǽAC�ϣ���ʱ���ӵײ�B��ǽ�˵ľ���Ϊ0.7�ף����������ӵ��ȶ��ԣ���Ҫ�����Ӷ���A��ǽ����0.4��A1���������ӵײ�B�����ƶ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ε����͵ij��ֱ���һԪ���η���x2��6x+8=0�ĸ�����������ε��ܳ�Ϊ�� ��
A.8
B.10
C.8��10
D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ���������У�AB=AC����D��б��BC�ϵ��е㣬��E��F�ֱ�ΪAB��AC�ϵĵ㣬��DE��DF��

��1������BE=a��CF=b������![]() +|b��5|=
+|b��5|=![]() +
+![]() ����BE��CF�ij���
����BE��CF�ij���
��2����֤��BE2+CF2=EF2��
��3���ڣ�1���������£�����DEF�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com