
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
分析 分别把各点坐标代入正比例函数的解析式进行一一验证即可.
解答 解:A、∵当x=2时,y=$\frac{2}{5}$×2=$\frac{4}{5}$≠5,∴此点不在正比例函数y=$\frac{2}{5}$x图象上,故本选项错误;
B、∵当x=5时,y=$\frac{2}{5}$×5=2,∴此点在正比例函数y=$\frac{2}{5}$x图象上,故本选项正确;
C、∵当x=2时,y=$\frac{2}{5}$×2=$\frac{4}{5}$≠-5,∴此点不在正比例函数y=$\frac{2}{5}$x图象上,故本选项错误;
D、∵当x=5时,y=$\frac{2}{5}$×5=2≠-2,∴此点不在正比例函数y=$\frac{2}{5}$x图象上,故本选项错误.
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,即一次函数图象上各点的坐标特点一定适合此函数的解析式.


科目:初中数学 来源: 题型:解答题
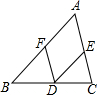 如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.
如图,点D在BC上,DE∥AB,交AC于点E,F是AB上的一个点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$=3$\sqrt{2}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | ($\sqrt{5}$+1)2=6 | D. | ($\sqrt{3}$+2)($\sqrt{3}$-2)=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
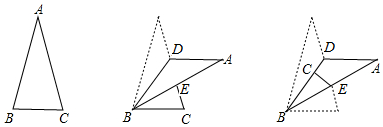
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
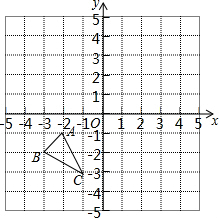 如图,在方格纸中,以O为旋转中心,将格点△ABC按顺时针方向旋转
如图,在方格纸中,以O为旋转中心,将格点△ABC按顺时针方向旋转查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对全国中学生心理健康现状的调查 | |
| B. | 谋批次汽车的抗重击能力的调查 | |
| C. | 春节联欢会晚会收视率的调查 | |
| D. | 对你所在的班级同学的身高情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
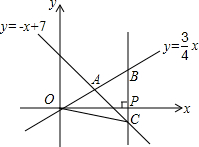 如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象交于点A.
如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{3}{4}$x与一次函数y=-x+7的图象交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
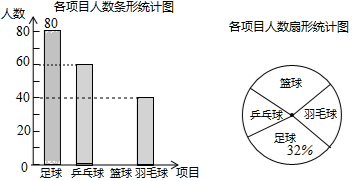
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com