
已知抛物线y=-x2+2mx-m2+2的顶点A在第一象限,过点A作AB⊥y轴于点B,C是线段AB上一点(不与点A、B重合),过点C作CD⊥x轴于点D并交抛物线于点P.

(1)若点C(1,a)是线段AB的中点,求点P的坐标;
(2)若直线AP交y轴的正半轴于点E,且AC=CP,求△OEP的面积S的取值范围.
|
解答:解:(1)依题意得顶点A的坐标为(2,a), 设P(1,n)据x=- 所以y=x2+4x-2,把P点的坐标代入得n=1, 即P点的坐标为(1,1) (2)把抛物线化为顶点式:y=-(x-m)2+2, 可知A(m,2),设C(n,2), 把n代入y=-(x-m)2+2得y=-(n-m)2+2, 所以P(n,-(n-m)2+2) ∵AC=CP ∴m-n=2+(m-n)2-2, 即m-n=(m-n)2, ∴m-n=0或m-n=1, 又∵C点不与端点A、B重合 ∴m≠n, 即m-n=1, 则A(m,2),P(m-1,1) 由AC=CP可得BE=AB ∵OB=2 ∴OE=2-m, ∴△OPE的面积S= ∴0<S< 点评:本题考查了二次函数的应用,解题的关键是正确的用字母表示出点的坐标,并利用题目的已知条件得到有关的方程或不等式,从而求得未知数的值或取值范围. 分析:(1)根据题意得顶点A的坐标为(2,a),然后设P(1,n)代入x=- (2)把抛物线化为顶点式:y=-(x-m)2+2,求得其顶点坐标,设C(n,2),然后表示出P(n,-(n-m)2+2)根据AC=CP求得m-n的值,然后表示出OB、OE的值从而表示出△OPE的面积,进而求得面积的取值范围. |


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
1.求b+c的值
2.若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
3.在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源:2011届广东省深圳市华富中学初三上学期期中数学卷 题型:解答题
已知抛物线y=-x2+mx-m+2.
(Ⅰ)若抛物线与x轴的两个交点A、B分别在原点的两侧,并且AB=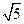 ,试求m的值;
,试求m的值;
(Ⅱ)设C为抛物线与y轴的交点,若抛物线上存在关于原点对称的两点M、N,并且 △MNC的面积等于27,试求m的值
查看答案和解析>>
科目:初中数学 来源:2010-2011学年度潍坊市高密七年级第二学期期末考试数学 题型:解答题
(11·兵团维吾尔)(8分)已知抛物线y=-x2+4x-3与x轴交于A、B两点(A
点在B点左侧),顶点为P.
(1)求A、B、P三点的坐标;
(2)在 直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
直角坐标系中,用列表描点法作出抛物线的图象,并根据图象写出x取何值时,函
数值大于零;
(3)将此抛物线的图象向下平移一个单位,请写出平称后图象的函数表达式.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建尤溪初中毕业学业质量检测数学试卷(解析版) 题型:解答题
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
1.求b+c的值
2.若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
3.在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年苏州市区九年级上学期期末考试数学卷 题型:填空题
(本题满分5分)已知抛物线y=-x2+bx+c,它与x轴的两个交点分别为(-1,0),(3,0),求此抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com