
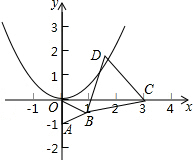
 如图,取点A(0,-1)作等边三角形AOB(点B在第四象限),点C是x轴上一动点,作等边三角形BCD,当点D恰好落在抛物线y=$\frac{1}{2}$x2上时,点D的坐标为($\sqrt{3}$+1,2+$\sqrt{3}$),($\sqrt{3}-1$,2-$\sqrt{3}$).
如图,取点A(0,-1)作等边三角形AOB(点B在第四象限),点C是x轴上一动点,作等边三角形BCD,当点D恰好落在抛物线y=$\frac{1}{2}$x2上时,点D的坐标为($\sqrt{3}$+1,2+$\sqrt{3}$),($\sqrt{3}-1$,2-$\sqrt{3}$). 分析 连接AD,根据等边三角形的性质得出OB=AB,BD=BC,∠ABO=∠DBC=60°,进而求得∠OBC=∠ABD,根据SAS证得△OBC≌△ABD,得出∠BAD=∠BOC=30°,即可证得直线AD的斜率为$\sqrt{3}$,即可得出直线AD的解析式,联立方程即可求得D的坐标.
解答  解:连接AD,
解:连接AD,
∵△AOB和△CBD是等边三角形,
∴OB=AB,BD=BC,∠ABO=∠DBC=60°,
∴∠ABO+∠OBD=∠DBC+∠OBD,
即∠OBC=∠ABD,
在△OBC和△ABD中,
$\left\{\begin{array}{l}{OB=AB}\\{∠OBC=∠ABD}\\{BC=BD}\end{array}\right.$
∴△OBC≌△ABD(SAS),
∴∠BAD=∠BOC,
∵∠AOB=60°,
∴∠BOC=30°,
∴∠BAD=30°
∴∠OAD=30°
∴直线AD的斜率为$\sqrt{3}$,
∴直线AD的解析式为y=$\sqrt{3}$x-1,
解$\left\{\begin{array}{l}{y=\sqrt{3}x-1}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\sqrt{3}+1}\\{y=2+\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\sqrt{3}-1}\\{y=2-\sqrt{3}}\end{array}\right.$,
∴D($\sqrt{3}$+1,2+$\sqrt{3}$),($\sqrt{3}-1$,2-$\sqrt{3}$)
故答案为($\sqrt{3}$+1,2+$\sqrt{3}$),($\sqrt{3}-1$,2-$\sqrt{3}$).
点评 本题考查了等边三角形的性质,三角形全等的判定和性质以及二次函数图象上点的坐标特征,求得直线AD的解析式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
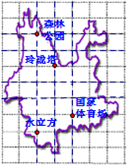 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2a}$ | B. | $\sqrt{3{a}^{2}}$ | C. | 2$\sqrt{a}$ | D. | $\sqrt{{a}^{4}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )| A. | (15,1) | B. | (15,-1) | C. | (30,1) | D. | (30,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com