
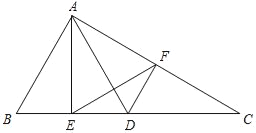
【题目】如图,在△ABC中,点D为边BC上一点,且AD=AB,AE⊥BC,垂足为点E.过点D作DF∥AB,交边AC于点F,连接EF,EF2=![]() BDEC.
BDEC.
(1)求证:△EDF∽△EFC;
(2)如果![]() ,求证:AB=BD.
,求证:AB=BD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用两边成比例夹角相等两个三角形相似即可证明;
(2)由△EDF∽△ADC,推出![]() =(
=(![]() )2=
)2=![]() ,推出
,推出![]() =
=![]() ,即ED=
,即ED=![]() AD,由此即可解决问题.
AD,由此即可解决问题.
(1)∵AB=AD,AE⊥BC,
∴BE=ED=![]() DB,
DB,
∵EF2=![]() BDEC,
BDEC,
∴EF2=EDEC,即得![]() =
=![]() ,
,
又∵∠FED=∠CEF,
∴△EDF∽△EFC;
(2)∵AB=AD,
∴∠B=∠ADB,
又∵DF∥AB,
∴∠FDC=∠B,
∴∠ADB=∠FDC,
∴∠ADB+∠ADF=∠FDC+∠ADF,即得∠EDF=∠ADC,
∵△EDF∽△EFC,
∴∠EFD=∠C,
∴△EDF∽△ADC,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴![]() =
=![]() ,即 ED=
,即 ED=![]() AD,
AD,
又∵ED=BE=![]() BD,
BD,
∴BD=AD,
∴AB=BD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]()
(1)如何将抛物线![]() 平移得到抛物线
平移得到抛物线![]() ?
?
(2)如图1,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,交抛物线
,交抛物线![]() 于另一点
于另一点![]() .请你在线段
.请你在线段![]() 上取点
上取点![]() ,过点
,过点![]() 作直线
作直线![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连接
,连接![]()

①若![]() ,求点
,求点![]() 的横坐标
的横坐标
②若![]() ,直接写出点
,直接写出点![]() 的横坐标
的横坐标
(3)如图2,![]() 的顶点
的顶点![]() 、
、![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在点
在点![]() 右边,两条直线
右边,两条直线![]() 、
、![]() 与抛物线
与抛物线![]() 均有唯一公共点,
均有唯一公共点,![]() 、
、![]() 均与
均与![]() 轴不平行.若
轴不平行.若![]() 的面积为2,设
的面积为2,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 与
与![]() 的数量关系
的数量关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情景:一节数学课后,老师布置了一道练习题:
如图1,已知Rt△ABC中,AC=BC,∠ABC=90°,CD⊥AB于点D,点E,F分别在AD和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF
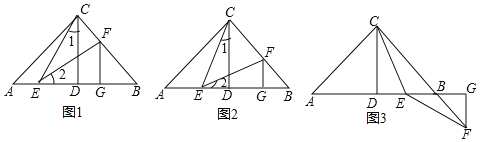
(1)阅读理解,完成解答:本题证明的思路可以用下列框图表示:
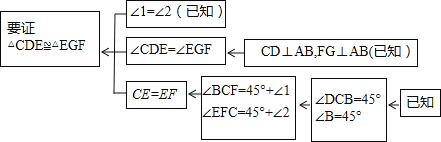
根据上述思路,请你完整地写出这道练习题的证明过程;
(2)特殊位置,证明结论:如图2,若CE平分∠ACD,其余条件不变,判断AE和BF的数量关系,并说明理由;
(3)知识迁移.探究发现:如图3,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上,且EC=EF,请直接写出BF与AE的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,将![]() 绕点
绕点![]() 旋转
旋转![]() 得到
得到![]() ,延长线于点
,延长线于点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,点![]() 是边
是边![]() 上任意一点(点
上任意一点(点![]() 与点
与点![]() 、
、![]() 不重合),连接
不重合),连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②当点![]() 是
是![]() 边中点时,恰有
边中点时,恰有![]() (
(![]() 为正整数),求
为正整数),求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
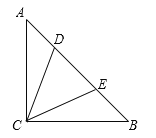
【题目】如图,在Rt△ABC中,∠ACB = 90°,![]() ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“新冠”疫情的影响,某销售商在网上销售![]() 、
、![]() 两种型号的“手写板”,获利颇丰.已知
两种型号的“手写板”,获利颇丰.已知![]() 型,
型,![]() 型手写板进价、售价和每日销量如表格所示:
型手写板进价、售价和每日销量如表格所示:
进价(元/个) | 售价(元/个) | 销量(个/日) | |
|
|
|
|
|
|
|
|
根据市场行情,该销售商对![]() 型手写板降价销售,同时对
型手写板降价销售,同时对![]() 型手写板提高售价,此时发现
型手写板提高售价,此时发现![]() 型手写板每降低
型手写板每降低![]() 元就可多卖
元就可多卖![]() 个,
个,![]() 型手写板每提高
型手写板每提高![]() 元就少卖
元就少卖![]() 个,要保持每天销售总量不变,设其中
个,要保持每天销售总量不变,设其中![]() 型手写板每天多销售
型手写板每天多销售![]() 个,每天总获利的利润为
个,每天总获利的利润为![]() 元
元
(1)求![]() 与
与![]() 之间的函数关系式并写出
之间的函数关系式并写出![]() 的取值范围;
的取值范围;
(2)要使每天的利润不低于![]() 元,直接写出
元,直接写出![]() 的取值范围;
的取值范围;
(3)该销售商决定每销售一个![]() 型手写板,就捐
型手写板,就捐![]() 元给
元给![]() 因“新冠疫情”影响的困难家庭,当
因“新冠疫情”影响的困难家庭,当![]() 时,每天的最大利润为
时,每天的最大利润为![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com