
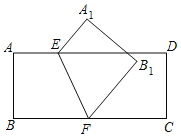
【题目】如图,点E、F分别在矩形ABCD的边AD、AB上,连接EF,四边形ABFE沿EF翻折能与四边形![]() 重合,且
重合,且![]() 与ED相交,若
与ED相交,若![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,点D、E、F分别在线段AB、BC、AC上,连接DE、EF、DM平分∠ADE交EF于点M,![]() ,求证:
,求证:![]() 。
。

证明:![]() (已知)
(已知)
又![]() (平角定义)
(平角定义)
∴∠2=∠BEM(____________________)
∴![]() __________(_________________________)
__________(_________________________)
![]() (_____________________________)
(_____________________________)
![]() (_____________________________)
(_____________________________)
又∵DM平分∠ADE(已知)
![]() (角平分线定义)
(角平分线定义)
![]() (等量代换)
(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,已知
轴上,已知![]() ,
,![]() ,
,![]() .
.

(1)平行四边形![]() 的面积为________;
的面积为________;
(2)如图1,点![]() 是
是![]() 边上的一点,若
边上的一点,若![]() 的面积是平行四边形
的面积是平行四边形![]() 的
的![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将![]() 绕点
绕点![]() 顺时针旋转,旋转得
顺时针旋转,旋转得![]() ,在整个旋转过程中,能否使以点
,在整个旋转过程中,能否使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若能,求点
为顶点的四边形是平行四边形?若能,求点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在□ABCD中,对角线AC、BD相交于点O.请找出图中的一对全等三角形,并给予证明;
(2)规定:一条弧所对的圆心角的度数作为这条弧的度数.
①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,求∠APB;
②一般地,在⊙O中,弦AC、BD相交于点P,若弧AB、弧CD分别为m°和n°,求∠APB.
(用m、n的代数式表示)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅以![]() 、
、![]() 两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克
两种食材,利用不同的搭配方式推出了两款健康餐,其中,甲产品每份含200克![]() 、200克
、200克![]() ;乙产品每份含200克
;乙产品每份含200克![]() 、100克
、100克![]() .甲、乙两种产品每份的成本价分别为
.甲、乙两种产品每份的成本价分别为![]() 、
、![]() 两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把
两种食材的成本价之和,若甲产品每份成本价为16元.店家在核算成本的时候把![]() 、
、![]() 两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元.
两种食材单价看反了,实际成本比核算时的成本多688元,如果每天甲销量的4倍和乙销量的3倍之和不超过120份,那么餐厅每天实际成本最多为______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学课上,老师出示了这样一个问题让学生探究:
已知:如图在△ABC中,点D 是BA边延长线上一动点,点F 在BC上,且![]() ,连接DF交AC于点E .
,连接DF交AC于点E .
(1)如图1,当点E恰为DF的中点时,请求出![]() 的值;
的值;
(2)如图2,当![]() 时,请求出
时,请求出![]() 的值(用含a的代数式表示).
的值(用含a的代数式表示).
思考片刻后,同学们纷纷表达自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以” .
请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问![]() 的值.
的值.


图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com