
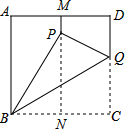
 如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.
如图所示,正方形纸片ABCD的边长为1,M,N分别是AD,BC的中点,将点C折叠到MN上,落在点P的位置,折痕为BQ.连结QP,PB,求PN,MP和CQ的长.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BP2-BN2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |


科目:初中数学 来源: 题型:
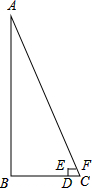 兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?
兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com