练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系中，将点P（－2，3）沿x轴方向向右平移3个单位得到点Q，则点Q的坐标是（ ）
    A.（－2，6）
    B.（－2，0）
    C.（1，3）
    D.（－5，3）

    【答案】C
    【解析】将点P（－2，3）向右平移3个单位得到点Q，即点Q的横坐标加3，纵坐标不变，则点Q的坐标是（1，3），故选C．
    根据坐标系内点的坐标的平移规律解题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线a经过点A（1，6），和点B（﹣3，﹣2）．

    （1）求直线a的解析式；

    （2）求直线与坐标轴的交点坐标；

    （3）求S△AOB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】﹣23的底数是________，指数是________，结果是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分式方程的解法:
    （1）方程两边都乘,去分母,化为方程;
    （2）解这个方程;
    （3）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】确定圆的位置，确定圆的大小.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30°，再向旗杆的方向前进16米，到达点D处（C、D、B三点在同一直线上），又测得旗杆顶端A的仰角为45°，请计算旗杆AB的高度（结果保留根号）

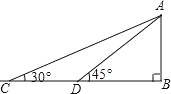
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    【初步思考】

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    【深入探究】

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    （1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据______，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    （2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    （3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

    （4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若______，则△ABC≌△DEF．

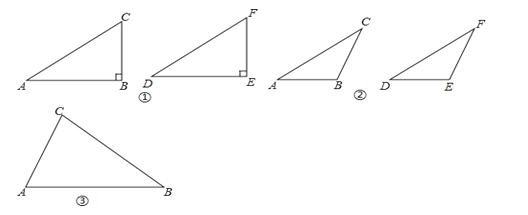
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着人们生活水平的提高，家用轿车越来越多地进入家庭，小明家中买了一辆小轿车，他连续记录了7天中每天行驶的路程(如下表)，以50 km为标准，多于50 km的记为“＋”，不足50 km的记为“－”，刚好50 km的记为“0”．

    第一天

    第二天

    第三天

    第四天

    第五天

    第六天

    第七天

    路程(km)

    －8

    －11

    －14

    0

    －16

    ＋41

    ＋8

    (1)请求出这七天中平均每天行驶多少千米？

    (2)若每天行驶100 km需用汽油6升，汽油价6.2元/升，请估计小明家一个月(按30天计)的汽油费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．

    （1）求证：AD=AF；

    （2）求证：BD=EF；

    （3）试判断四边形ABNE的形状，并说明理由．

    查看答案和解析>>

    同步练习册答案