
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?

【答案】解法一:设矩形温室的宽为xm,则长为2xm.根据题意,得
(x﹣2)(2x﹣4)=288.
解这个方程,得x1=﹣10(不合题意,舍去),x2=14.
所以x=14,2x=2×14=28.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
解法二:设矩形温室的长为xm,则宽为![]() xm.根据题意,得
xm.根据题意,得
(![]() x﹣2)(x﹣4)=288.
x﹣2)(x﹣4)=288.
解这个方程,得x1=﹣20(不合题意,舍去),x2=28.
所以x=28,![]() x=
x=![]() ×28=14.
×28=14.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
【解析】本题有多种解法.设的对象不同所列的一元二次方程不同.一般情况下当两个量之比为a:b时,则设它们分别为ax和bx.


科目:初中数学 来源: 题型:
【题目】已知,关于x的方程x2+2x-k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若x1,x2是这个方程的两个实数根,求![]() 的值;
的值;
(3)根据(2)的结果你能得出什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内部的一定点,M是AB边上一动点,连接MP并延长与矩形ABCD的一边交于点N,连接AN.已知AB=6cm,设A,M两点间的距离为xcm,M,N两点间的距离为y1cm,A,N两点间的距离为y2cm.小欣根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小欣的探究过程,请补充完整;
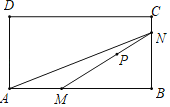
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.30 | 5.40 |
| 4.22 | 3.13 | 3.25 | 4.52 |
y2/cm | 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐标系xOy中,描出以补全后的表中各组对应值所对应的点(x,y1),并画出函数y1的图象;
(3)结合函数图象,解决问题:当△AMN为等腰三角形时,AM的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
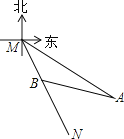
【题目】如图,射线MN表示一艘轮船的航行路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,A处到M处为100海里.
(1)求点A到航线MN的距离;
(2)在航线MN上有一点B,且∠MAB=15°,若轮船的速度为50海里/时,求轮船从M处到B处所用时间为多少小时?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.
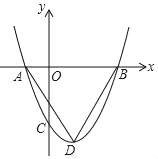
(1)求△ABD的面积;
(2)点P是抛物线上的一动点,且点P在x轴上方,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
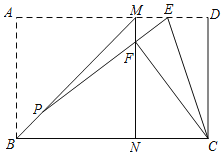
【题目】如图,在矩形纸片ABCD中,将AB沿BM翻折,使点A落在BC上的点N处,BM为折痕,连接MN;再将CD沿CE翻折,使点D恰好落在MN上的点F处,CE为折痕,连接EF并延长交BM于点P,若AD=8,AB=5,则线段PE的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
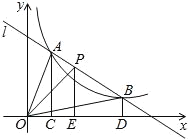
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
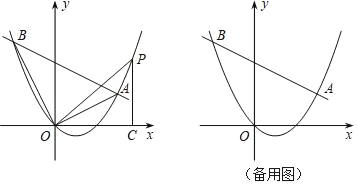
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com