
”¾ĢāÄæ”æĪŅŹŠÄ³¹¤ŅÕ³§ĪŖÅäŗĻ±±¾©°ĀŌĖ£¬Éč¼ĘĮĖŅ»æī³É±¾ĪŖ20ŌŖØM¼žµÄ¹¤ŅÕĘ·Ķ¶·ÅŹŠ³”½ųŠŠŹŌĻś£®¾¹żµ÷²é£¬µĆµ½ČēĻĀŹż¾Ż£ŗ
ĻśŹŪµ„¼Ūx£ØŌŖ/¼ž£© | ” | 30 | 40 | 50 | 60 | ” |
ĆæĢģĻśŹŪĮæy£Ø¼ž£© | ” | 500 | 400 | 300 | 200 | ” |
£Ø1£©°ŃÉĻ±ķÖŠx”¢yµÄø÷×é¶ŌÓ¦Öµ×÷ĪŖµćµÄ×ų±ź£¬ŌŚĻĀĆęµÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠĆč³öĻąÓ¦µÄµć£¬²ĀĻėyÓėxµÄŗÆŹż¹ŲĻµ£¬²¢Ēó³öŗÆŹż¹ŲĻµŹ½£» 
£Ø2£©µ±ĻśŹŪµ„¼Ū¶ØĪŖ¶ąÉŁŹ±£¬¹¤ŅÕ³§ŹŌĻśøĆ¹¤ŅÕĘ·ĆæĢģ»ńµĆµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ£ØĄūČó=ĻśŹŪ×ܼŪ©³É±¾×ܼŪ£©
£Ø3£©µ±µŲĪļ¼Ū²æĆŹę¶Ø£¬øĆ¹¤ŅÕĘ·ĻśŹŪµ„¼Ū×īøß²»Äܳ¬¹ż45ŌŖ/¼ž£¬ÄĒĆ“ĻśŹŪµ„¼Ū¶ØĪŖ¶ąÉŁŹ±£¬¹¤ŅÕ³§ŹŌĻśøĆ¹¤ŅÕĘ·ĆæĢģ»ńµĆµÄĄūČó×ī“ó£æ
”¾“š°ø”æ
£Ø1£©½ā£ŗČēĶ¼ĖłŹ¾£ŗ
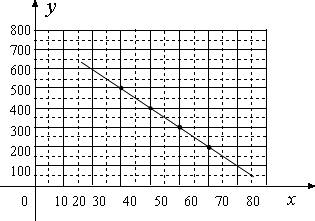
ÓÉĶ¼æɲĀĻėyÓėxŹĒŅ»“ĪŗÆŹż¹ŲĻµ£¬
ÉčÕāøöŅ»“ĪŗÆŹżĪŖy=kx+b£Øk”Ł0£©
”ßÕāøöŅ»“ĪŗÆŹżµÄĶ¼Ļó¾¹ż£Ø30£¬500£©
£Ø40£¬400£©ÕāĮ½µć£¬
”ą ![]() ½āµĆ
½āµĆ ![]()
”ąŗÆŹż¹ŲĻµŹ½ŹĒ£ŗy=©10x+800£Ø20”Üx”Ü80£©
£Ø2£©½ā£ŗÉč¹¤ŅÕ³§ŹŌĻśøĆ¹¤ŅÕĘ·ĆæĢģ»ńµĆµÄĄūČóŹĒWŌŖ£¬ŅĄĢāŅāµĆ
W=£Øx©20£©£Ø©10x+800£©
=©10x2+1000x©16000
=©10£Øx©50£©2+9000£¬£Ø20”Üx”Ü80£©
”ąµ±x=50Ź±£¬WÓŠ×ī“óÖµ9000£®
ĖłŅŌ£¬µ±ĻśŹŪµ„¼Ū¶ØĪŖ50ŌŖØM¼žŹ±£¬¹¤ŅÕ³§ŹŌĻśøĆ¹¤ŅÕĘ·ĆæĢģ»ńµĆµÄĄūČó×ī“ó£¬×ī“óĄūČóŹĒ9000ŌŖ
£Ø3£©½ā£ŗ¶ŌÓŚŗÆŹżW=©10£Øx©50£©2+9000£¬µ±x”Ü45Ź±£¬
WµÄÖµĖę×ÅxÖµµÄŌö“ó¶ųŌö“ó£¬
”ąĻśŹŪµ„¼Ū¶ØĪŖ45ŌŖØM¼žŹ±£¬¹¤ŅÕ³§ŹŌĻśøĆ¹¤ŅÕĘ·ĆæĢģ»ńµĆµÄĄūČó×ī“ó
”¾½āĪö”æ£Ø1£©Ćčµć£¬ÓÉĶ¼æɲĀĻėyÓėxŹĒŅ»“ĪŗÆŹż¹ŲĻµ£¬ČĪŃ”Į½µćĒó±ķ“ļŹ½£¬ŌŁŃéÖ¤²ĀĻėµÄÕżČ·ŠŌ£»£Ø2£©ĄūČó=ĻśŹŪ×ܼŪ©³É±¾×ܼŪ=µ„¼žĄūČó”ĮĻśŹŪĮ森¾Ż“ĖµĆ±ķ“ļŹ½£¬ŌĖÓĆŠŌÖŹĒó×īÖµ£»£Ø3£©øł¾Ż×Ō±äĮæµÄȔֵ·¶Ī§½įŗĻŗÆŹżĶ¼Ļó½ā“š£®


 Š”ѧæĪŹ±×÷ŅµČ«ĶØĮ·°øĻµĮŠ“š°ø
Š”ѧæĪŹ±×÷ŅµČ«ĶØĮ·°øĻµĮŠ“š°ø ½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø
½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø
µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖׄהčó¾»É½ĪÄ»ÆŅÕŹõ½ŚµÄÉĢ»ś£¬Ä³ÉĢµź¾ö¶Ø¹ŗ½ųA”¢BĮ½ÖÖŅÕŹõ½Ś¼ĶÄīĘ·£®Čō¹ŗ½ųAÖÖ¼ĶÄīĘ·8¼ž£¬BÖÖ¼ĶÄīĘ·3¼ž£¬ŠčŅŖ950ŌŖ£»Čō¹ŗ½ųAÖÖ¼ĶÄīĘ·5¼ž£¬BÖÖ¼ĶÄīĘ·6¼ž£¬ŠčŅŖ800ŌŖ£®
£Ø1£©Ēó¹ŗ½ųA”¢BĮ½ÖÖ¼ĶÄīĘ·Ć漞ø÷Šč¶ąÉŁŌŖ£æ
£Ø2£©ČōøĆÉĢµź¾ö¶Ø¹ŗ½ųÕāĮ½ÖÖ¼ĶÄīĘ·¹²100¼ž£¬æ¼ĀĒŹŠ³”ŠčĒóŗĶ׏½šÖÜ×Ŗ£¬ÓĆÓŚ¹ŗĀņÕā100¼ž¼ĶÄīĘ·µÄ׏½š²»ÉŁÓŚ7500ŌŖ£¬µ«²»³¬¹ż7650ŌŖ£¬ÄĒĆ“øĆÉĢµź¹²ÓŠ¼øÖÖ½ų»õ·½°ø£æ
£Ø3£©ČōĻśŹŪĆ漞AÖÖ¼ĶÄīĘ·æÉ»ńĄūČó20ŌŖ£¬Ć漞BÖÖ¼ĶÄīĘ·æÉ»ńĄūČó30ŌŖ£¬ŌŚµŚ£Ø2£©ĪŹµÄø÷ÖÖ½ų»õ·½°øÖŠ£¬ÄÄŅ»ÖÖ·½°ø»ńĄū×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
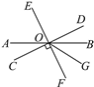
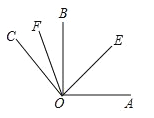
”¾ĢāÄæ”æČēĶ¼£¬Ö±ĻßAB£¬CD£¬EF½»ÓŚµćO£¬OGĘ½·Ö”ĻBOF£¬ĒŅCD”ĶEF£¬”ĻAOE£½64”ć£¬Ēó”ĻAOF£¬”ĻDOGµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµēŹÓĢØ”°×ß»ł²ć”±ĄøÄæµÄŅ»Ī»¼ĒÕß³ĖĘū³µø°320kmĶāµÄÅ©“å²É·Ć£¬Č«³ĢµÄĒ°Ņ»²æ·ÖĪŖøßĖŁ¹«
Ā·£¬ŗóŅ»²æ·ÖĪŖĻē“幫Ā·£®ČōĘū³µŌŚøßĖŁ¹«Ā·ŗĶĻē“幫Ā·ÉĻ·Ö±šŅŌijŅ»ĖŁ¶ČŌČĖŁŠŠŹ»£¬Ęū³µŠŠŹ»µÄĀ·³Ģy£Øµ„Ī»£ŗkm£©ÓėŹ±¼äx£Øµ„Ī»£ŗh£©Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬ŌņĻĀĮŠ½įĀŪÕżČ·µÄŹĒ£Ø £©
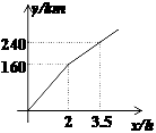
A£®Ęū³µŌŚøßĖŁ¹«Ā·ÉĻµÄŠŠŹ»ĖŁ¶ČĪŖ100km/h
B£®Ļē“幫Ā·×ܳ¤ĪŖ90km
C£®Ęū³µŌŚĻē“幫Ā·ÉĻµÄŠŠŹ»ĖŁ¶ČĪŖ60km/h
D£®øĆ¼ĒÕßŌŚ³ö·¢ŗó5hµ½“ļ²É·ĆµŲ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖćĢā”£
£Ø1£©¼ĘĖć£ŗ ![]() .
.
£Ø2£©½ā²»µČŹ½£ŗ4x+5”Ü2£Øx+1£©.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŅŃÖŖ”ĻAOB=90”ć,”ĻEOF=60”ć£¬OEĘ½·Ö”ĻAOB£¬OFĘ½·Ö”ĻBOC£¬Ēó”ĻCOBŗĶ”ĻAOCµÄ¶ČŹż.£ØŠ“³ö±ŲŅŖ¹ż³Ģ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() ĪŖĻ߶Ī
ĪŖĻ߶Ī![]() ÉĻŅ»¶Æµć£¬·Ö±š¹żµć
ÉĻŅ»¶Æµć£¬·Ö±š¹żµć![]() ×÷
×÷![]() £¬
£¬![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .ŅŃÖŖ
.ŅŃÖŖ![]() £¬Éč
£¬Éč![]() .
.
(1)ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾
µÄ“śŹżŹ½±ķŹ¾![]() µÄÖµ;
µÄÖµ;
(2)Ģ½¾æ:µ±µć![]() Āś×ćŹ²Ć“Ģõ¼žŹ±£¬
Āś×ćŹ²Ć“Ģõ¼žŹ±£¬![]() µÄÖµ×īŠ”?×īŠ”ÖµŹĒ¶ąÉŁ?
µÄÖµ×īŠ”?×īŠ”ÖµŹĒ¶ąÉŁ?
(3)øł¾Ż(2)ÖŠµÄ½įĀŪ£¬Ēė¹¹ŌģĶ¼ŠĪĒ󓜏żŹ½![]() µÄ×īŠ”Öµ.
µÄ×īŠ”Öµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµēĘ÷¹«Ė¾¼Ę»®×°ŌĖ¼×”¢ŅŅ”¢±ūČżÖÖ¼Ņµēµ½Å©“åĻśŹŪ(¹ę¶ØĆæĮ¾Ęū³µ°“¹ę¶ØĀśŌŲ£¬ĒŅĆæĮ¾Ęū³µÖ»ÄÜ×°Ķ¬Ņ»ÖÖ¼Ņµē)£®ĻĀ±ķĖłŹ¾ĪŖ×°ŌĖ¼×”¢ŅŅ”¢±ūČżÖÖ¼ŅµēµÄĢØŹż¼°ĄūČó£®
¼× | ŅŅ | ±ū | |
ĆæĮ¾Ęū³µÄÜ×°ŌĖµÄĢØŹż | 40 | 20 | 30 |
ĆæĢؼŅµēæÉ»ńĄūČó(ĶņŌŖ) | 0.05 | 0.07 | 0.04 |
(1)ČōÓĆ8Į¾Ęū³µ×°ŌĖŅŅ”¢±ūĮ½ÖÖ¼Ņµē190Ģص½AµŲĻśŹŪ£¬ĪŹ×°ŌĖŅŅ”¢±ūµÄĘū³µø÷¶ąÉŁĮ¾£®
(2)¼Ę»®ÓĆ20Į¾Ęū³µ×°ŌĖ¼×”¢ŅŅ”¢±ūČżÖÖ¼Ņµē720Ģص½BµŲĻśŹŪ£¬ČēŗĪ°²ÅÅ×°ŌĖ£¬æÉŹ¹¹«Ė¾»ńµĆ36.6ĶņŌŖµÄĄūČó£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŗÓ°Óŗį¶ĻĆę±³Ė®ĘĀABµÄĘĀ½ĒŹĒ45”ć£¬±³Ė®ĘĀAB³¤¶ČĪŖ20 ![]() Ć×£¬ĻÖŌŚĪŖ¼Ó¹ĢµĢ°Ó£¬½«Š±ĘĀABøijÉĘĀ¶ČĪŖ1£ŗ2µÄŠ±ĘĀAD”¾±ø×¢£ŗAC”ĶCB”æ
Ć×£¬ĻÖŌŚĪŖ¼Ó¹ĢµĢ°Ó£¬½«Š±ĘĀABøijÉĘĀ¶ČĪŖ1£ŗ2µÄŠ±ĘĀAD”¾±ø×¢£ŗAC”ĶCB”æ 
£Ø1£©Ēó¼Ó¹Ģ²æ·Ö¼“”÷ABDµÄŗį½ŲĆęµÄĆ껿£»
£Ø2£©ČōøƵĢ°ÓµÄ³¤¶ČĪŖ100Ć×£¬Ä³¹¤³Ģ¶Ó³Š°üĮĖÕāŅ»¼Ó¹ĢµÄĶĮŹÆ·½¹¤³Ģ£¬ĪŖĒĄŌŚŌŚŃ“ĘŚµ½Ą“Ö®¼ŹĢįĒ°Ķź³ÉÕāŅ»¹¤³Ģ£¬ĻÖŌŚĆæĢģĶź³ÉµÄĶĮ·½±ČŌ¼Ę»®Ōö¼Ó25%£¬ÕāŃłŹµ¼Ź±ČŌ¼Ę»®ĢįĒ°10ĢģĶź³ÉĮĖ£¬ĒóŌ¼Ę»®ĆæĢģĶź³ÉµÄĶĮ·½£®”¾ĢįŹ¾ĶĮŹÆ·½=ŗį½ŲĆęxµĢ°Ó³¤¶Č”æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com