
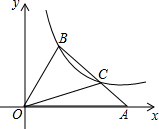
 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B、C在反比例函数y=$\frac{k}{x}$(x>0)的图象上,若△OAB的面积等于6,则k的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 设A的坐标是(a,0),设B的坐标是(m,n).则mn=k,C的坐标是($\frac{m+a}{2}$,$\frac{n}{2}$),然后根据C在反比例函数上,则$\frac{m+a}{2}$•$\frac{n}{2}$=k,再根据三角形的面积公式可得an=12,据此即可求解.
解答 解:设A的坐标是(a,0),设B的坐标是(m,n).则mn=k.
∵C是AB的中点,
∴C的坐标是($\frac{m+a}{2}$,$\frac{n}{2}$).
∵C在反比例函数上,
∴$\frac{m+a}{2}$•$\frac{n}{2}$=k,即(m+a)n=4k,mn+an=4k.
∵△OAB的面积是6,
∴$\frac{1}{2}$an=6,即an=12,
∴k+12=4k,
解得k=4.
故选B.
点评 本题考查了求反比例函数的解析式,正确设出未知数,转化为k的关系是关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x>2m\\ x<2n\end{array}\right.$ | B. | $\left\{\begin{array}{l}x<m-n\\ x<m+n\end{array}\right.$ | C. | $\left\{\begin{array}{l}x>m\\ x>n-1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x<m-2n\\ x>-n\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com