
 如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为$\frac{5}{2}$.
如图,AB是⊙O的直径,CD为⊙O的一条弦,CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为$\frac{5}{2}$. 科目:初中数学 来源: 题型:填空题
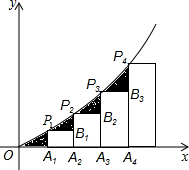 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
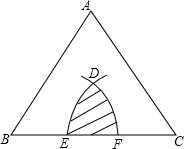 正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分的面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是多少?
正△ABC的边长是4,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分的面积为S,当2$\sqrt{2}$≤r≤4时,S的取值范围是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
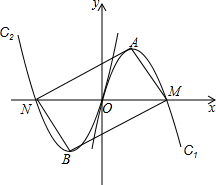 如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是y=-$\sqrt{3}$x2+2$\sqrt{3}$x和y=$\sqrt{3}$x2+2$\sqrt{3}$x(答案不唯一).
如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是y=-$\sqrt{3}$x2+2$\sqrt{3}$x和y=$\sqrt{3}$x2+2$\sqrt{3}$x(答案不唯一).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com