
【题目】如图,△ABC中,AB= ![]() ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 .
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 . 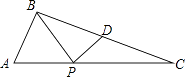
【答案】2或5﹣ ![]()
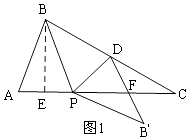
【解析】解:分两种情况:①当点B′在AC的下方时,如图1,
∵D是BC中点,
∴S△BPD=S△PDC,
∵S△PDF= ![]() S△BPD,
S△BPD,
∴S△PDF= ![]() S△PDC,
S△PDC,
∴F是PC的中点,
∴DF是△BPC的中位线,
∴DF∥BP,
∴∠BPD=∠PDF,
由折叠得:∠BPD=∠B′PD,
∴∠B′PD=∠PDF,
∴PB′=B′D,
即PB=BD,
过B作BE⊥AC于E,
Rt△ABE中,tan∠A= ![]() =2,
=2,
∵AB= ![]() ,
,
∴AE=1,BE=2,
∴EC=5﹣1=4,
由勾股定理得:BC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵D为BC的中点,
∴BD= ![]() ,
,
∴PB=BD= ![]() ,
,
在Rt△BPE中,PE=1,
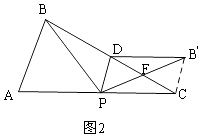
∴AP=AE+PE=1=1=2;②当点B'在AC的上方时,如图2,连接B′C,
同理得:F是DC的中点,F是PB′的中点,
∴DF=FC,PF=FB′,
∴四边形DPCB′是平行四边形,
∴PC=B′D=BD= ![]() ,
,
∴AP=5﹣ ![]() ,
,
综上所述,AP的长为2或5﹣ ![]() ;
;
所以答案是:2或5﹣ ![]() .
.
【考点精析】利用翻折变换(折叠问题)和解直角三角形对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
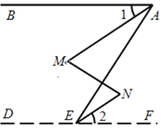
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE(______).
∴∠BAE=∠AEF(______).
又∵∠1=∠2(已知)
∴ ∠BAE∠1=∠AEF_____(等式性质),即 ∠MAE = ∠NEA .
∴_______∥______(______).
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一根长为5米的竹竿AB斜立于墙MN的右侧,底端B与墙角N 的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系的大致图象是( )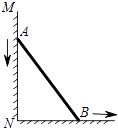
A.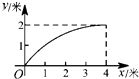
B.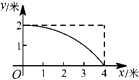
C.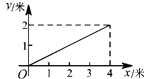
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)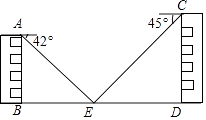
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A1,A2,A3,…,An(n为正整数)都在数轴上,点A1在原点O的左边,且A1O=1;点A2在点A1的右边,且A2A1=2;点A3在点A2的左边,且A3A2=3;点A4在点A3的右边,且A4A3=4;…,依照上述规律,点A2018,A2019所表示的数分别为( )
A. 2018,﹣2019B. 1009,﹣1010C. ﹣2018,2019D. ﹣1009,1010
查看答案和解析>>
科目:初中数学 来源: 题型:
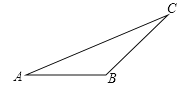
【题目】画图并填空:
①画出图中△ABC的高AD(标注出点D的位置);
②画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
③根据“图形平移”的性质,得BB1=_____cm,AC与A1C1的位置关系是_____,数量关系是:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
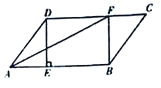
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com