
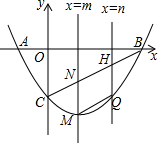
 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值.
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线x=m(m>0),直线x=n(n>0)(m<n)分别交线段BC于N点、H点,交抛物线于M点、Q点.当NH∥MQ时,求m+n的值. 分析 作QL⊥MN于点L,已知M和N的坐标分别是(m,m2-2m-3),(n,n2-2n-3),先证明QL=ML,即可列方程求得m、n的关系即可求解.
解答 解:在y=x2-2x-3中,令x=0,则y=-3,即C的坐标是(0,-3),OC=3,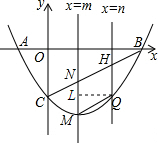
在y=x2-2x-3中,令y=0,则x2-2x-3=0,解得:x=-1或3,
则A的坐标是(-1,0),B的坐标是(3,0),OB=3,
则OB=OC.
作QL⊥MN于点L.
由题意得M(m,m2-2m-3),Q(n,n2-2n-3).
∵MQ∥BC,OB=OC,
∴∠OCB=∠OBC=45°,
∴∠NMQ=∠CNM=∠OCB=45°,
∴QL=ML,
∴n-m=n2-2n-3-(m2-2m-3),
n-m=(n+m)(n-m)-2(n-m),
∵n-m≠0,
∴1=m+n-2,
则m+n=3.
点评 本题考查了二次函数与坐标轴的交点以及两直线平行的条件,根据平行条件得到n-m=n2-2n-3-(m2-2m-3)是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
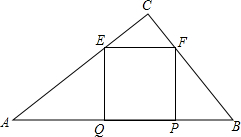 如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.
如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 利川4.2℃ | B. | 广州13.5℃ | C. | 北京-4.8℃ | D. | 兰州-3.4℃ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com