
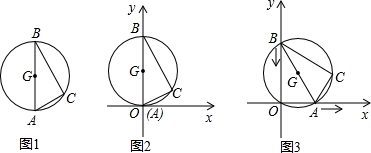
分析 由于在运动过程中,原点O始终在⊙G上,则弧AC的长保持不变,弧AC所对应的圆周角∠AOC保持不变,等于∠XOC,故点C在与x轴夹角为∠ABC的射线上运动.顶点C的运动轨迹应是一条线段,且点C移动到图中C2位置最远,然后又慢慢移动到C3结束,点C经过的路程应是线段C1C2+C2C3.
解答 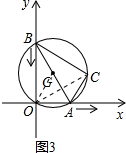 解:如图3,连接OG.
解:如图3,连接OG.
∵∠AOB是直角,G为AB中点,
∴GO=$\frac{1}{2}$AB=半径,
∴原点O始终在⊙G上.
∵∠ACB=90°,AB=2,AC=1,
∴BC=$\sqrt{3}$.
连接OC.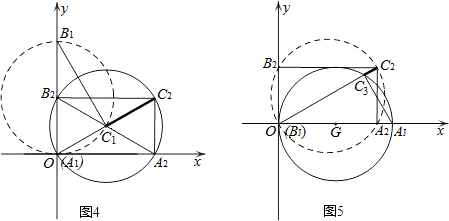 则∠AOC=∠ABC,
则∠AOC=∠ABC,
∴tan∠AOC=$\frac{AC}{BC}$=$\frac{\sqrt{3}}{3}$,
∴点C在与x轴夹角为∠AOC的射线上运动.
如图4,C1C2=OC2-OC1=2-1=1;
如图5,C2C3=OC2-OC3=2-$\sqrt{3}$;
∴总路径为:C1C2+C2C3=1+2-$\sqrt{3}$=3-$\sqrt{3}$.
故答案为:3-$\sqrt{3}$.
点评 此题主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.


科目:初中数学 来源: 题型:选择题
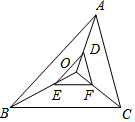 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
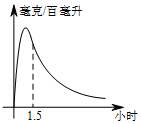 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
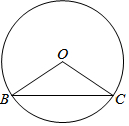 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,2cm,3.5cm | B. | 3cm,4cm,6cm | C. | 4cm,5cm,9cm | D. | 3cm,3cm,6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com