
 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:分析 (1)①根据限变点的定义直接得出答案;
②点(-1,-2)在反比例函数图象上,点(-1,-2)的限变点为(-1,2),据此得到答案;
(2)根据题意可知y=-x+3(x≥-2)图象上的点P的限变点必在函数y=$\left\{\begin{array}{l}{-x+3,x≥1}\\{x-3,-2≤x<1}\end{array}\right.$的图象上,结合图象即可得到答案.
解答 解:(1)①根据限变点的定义可知点($\sqrt{3}$,1)的限变点的坐标为($\sqrt{3}$,1);
②(-1,-2)是函数y=$\frac{2}{x}$图象上的点,(-1,-2)限变点为(-1,2),即这个点是点B.
(2)依题意,y=-x+3(x≥-2)图象上的点P的限变点必在函数y=$\left\{\begin{array}{l}{-x+3,x≥1}\\{x-3,-2≤x<1}\end{array}\right.$的图象上.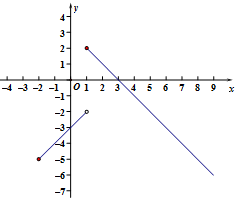
∴b′≤2,即当x=1时,b′取最大值2.
当b′=-2时,-2=-x+3.
∴x=5.
当b′=-5时,-5=x-3或-5=-x+3.
∴x=-2或x=8.
∵-5≤b′≤2,
由图象可知,k的取值范围是5≤k≤8,
故答案为:5≤k≤8.
点评 本题主要考查了二次函数的综合题,解答本题的关键是熟练掌握新定义“限变点”,解答此题还需要掌握二次函数的性质以及最值的求解,此题有一定的难度.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
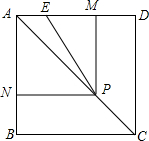 如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com