
【题目】如图,已知OE是∠AOC的角平分线,OD是∠BOC的角平分线.
(1)若∠AOC=120°,∠BOC=30°,求∠DOE的度数;
(2)若∠AOB=90°,∠BOC=α,求∠DOE的度数.

【答案】(1) 45°;(2) 45°.
【解析】(1)根据角平分线定义,先求∠AOE= ![]() ∠AOC , ∠COD=
∠AOC , ∠COD= ![]() ∠BOC ,
∠BOC ,
由∠DOE=∠AOC-∠AOE -∠COD可求的结果;
(2)根据角平分线定义,得∠AOE= ![]() (90°+α),∠COD=
(90°+α),∠COD= ![]() α ,再根据∠DOE=∠AOC - ∠AOE-∠COD可求得结果.
α ,再根据∠DOE=∠AOC - ∠AOE-∠COD可求得结果.
解:(1)∵ OE是∠AOC的角平分线,OD是∠BOC的角平分线.
∴ ∠AOE= ![]() ∠AOC ,
∠AOC ,
∠COD= ![]() ∠BOC ,
∠BOC ,
∵∠AOC=120°,∠BOC=30°
∴ ∠AOE= ![]() ×120° =60°
×120° =60°
∠COD= ![]() × 30°= 15°
× 30°= 15°
∠DOE=∠AOC - ∠AOE - ∠COD
=120°- 60°-15°= 45°.
(2)∵ ∠AOB=90°,∠BOC=α
∴ ∠AOC = 90°+α
∵ OE是∠AOC的角平分线,OD是∠BOC的角平分线.
∴∠AOE= ![]() ∠AOC , ∠COD=
∠AOC , ∠COD= ![]() ∠BOC
∠BOC
∠AOE= ![]() (90°+α),∠COD=
(90°+α),∠COD= ![]() α
α
∠DOE=∠AOC - ∠AOE-∠COD
= (90°+α)- ![]() (90°+α)-
(90°+α)- ![]() α = 45°
α = 45°


科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并写出A、C两点的坐标;
(2)根据(1)的坐标系作出与△ABC关于x轴对称的图形△A1B1C1,并写出B1、C1两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽有5张写着不同数的卡片,请你按要求抽出卡片,完成下列各题:

(1)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相乘再相除的结果最大?最大值是多少?
(2)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相除再相乘的结果最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OM是∠AOC的角平分线,ON是∠BOC的角平分线;
(1)当∠BOC=40°时,求∠MON的大小?
(2)当∠BOC的大小发生变化时,∠MON的大小是否发生改变?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)﹣![]() a2bc+
a2bc+![]() cba2
cba2
(2)7ab﹣3a2b2+7+8ab2+3a2b2﹣3﹣7ab
(3)(﹣x+2x2+5)+(4x2﹣3﹣6x)
(4)(2x2﹣![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
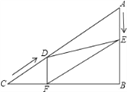
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中, B(0,8),D(10,0),一次函数y=![]() x+
x+![]() 的图象过C(16,n),与x轴交于A点。
的图象过C(16,n),与x轴交于A点。
(1)求证:四边形ABCD为平行四边形;
(2)将△AOB绕点O顺时针旋转,旋转得△A1OB1,问:能否使以点O、A1、D、B1为顶点的四边形是平行四边形?若能,求点A1的坐标;若不能,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com