
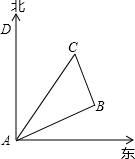
 如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500
如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500 m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点.
m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点.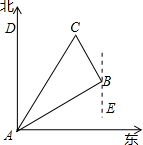
 m,
m,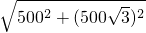 =1 000(m);
=1 000(m);

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
 m,出手后的铅球沿一段抛物线弧运行,当运行
m,出手后的铅球沿一段抛物线弧运行,当运行 到高度y=3m时,水平距离是x=4m.
到高度y=3m时,水平距离是x=4m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙M中,
如图,在⊙M中, 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
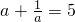 ,试求
,试求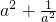 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com