
分析 仿照例子,设S=1+3+32+33+34+…+3n,由此可得出3S=3+32+33+34+…+3n+1,两者做差即可得出3S-S=3n+1-1,由此即可得出结论.
解答 解:设S=1+3+32+33+34+…+3n①(其中n为正整数),
将①×3得:3S=3+32+33+34+…+3n+1②,
由②-①得:3S-S=3n+1-1,即S=$\frac{{3}^{n+1}-1}{2}$,
故1+3+32+33+34+…+3n=$\frac{{3}^{n+1}-1}{2}$(其中n为正整数).
点评 本题考查了规律型中的数字的变化类,解题的关键是仿照例子计算1+3+32+33+…+3n.本题属于基础题,难度不大,本题其实是等比数列的求和公式,但初中未接触过该方面的知识,需要借助于错位相减法来求出结论.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x=4 | B. | x=5 | C. | x=6 | D. | x=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
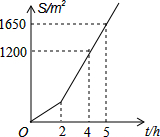 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 300m2 | B. | 150m2 | C. | 330m2 | D. | 450m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com