
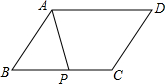
 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,分析 (1)求出$\widehat{AB}$,$\widehat{BP}$,根据$\widehat{AB}$=$\widehat{AB}$+$\widehat{BP}$,即可求出$\overrightarrow{AP}$,
(2)如图$\overrightarrow{AB}-\overrightarrow{BP}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$=$\overrightarrow{EB}$.
解答 解:(1)在平行四边形ABCD中,$\overrightarrow{BA}=\overrightarrow{CD}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{AD}=\overrightarrow{b}$,
∵点P是BC的中点,
∴$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}$,
∴$\overrightarrow{AB}=-\overrightarrow{BA}$,$\overrightarrow{AB}+\overrightarrow{BP}=\overrightarrow{AP}$
∴$\overrightarrow{AP}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,
(2)如图:$\overrightarrow{AB}-\overrightarrow{BP}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$=$\overrightarrow{EB}$,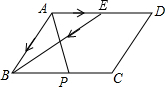
$\overrightarrow{EB}$就是所求的向量.
故答案为:$-\overrightarrow a+\frac{1}{2}\overrightarrow b$.
点评 本题是基础题,考查向量的加减法的运算,注意向量的和与差后仍然是一个向量.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com