
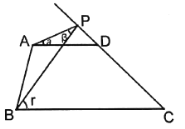
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AC£½BC£½2£¬”ĻC£½90”ć£¬½«Ņ»æéµČŃüČż½Ē°åµÄÖ±½Ē¶„µć·ÅŌŚŠ±±ßABµÄÖŠµćP“¦£¬½«Čż½Ē°åČʵćPŠż×Ŗ£¬Čż½Ē°åµÄĮ½Ö±½Ē±ß·Ö±š½»ÉäĻßAC”¢CBÓŚD”¢EĮ½µć£®ČēĶ¼¢Ł”¢¢Ś”¢¢ŪŹĒŠż×ŖČż½Ē°åµĆµ½µÄĶ¼ŠĪÖŠµÄ3ÖÖĒéæö£¬ŃŠ¾æ£ŗ
£Ø1£©Čż½Ē°åČʵćPŠż×Ŗ£¬¹Ū²ģĻ߶ĪPDÓėPEÖ®¼äÓŠŹ²Ć“ŹżĮæ¹ŲĻµ£æ½įŗĻĶ¼¢ŚĖµĆ÷ĄķÓÉ£®
£Ø2£©Čż½Ē°åČʵćPŠż×Ŗ£¬”÷PCEŹĒ·ńÄܳÉĪŖµČŃüČż½ĒŠĪ£æČōÄÜ£¬Öø³öĖłÓŠĒéæö£ØÖ±½ÓŠ““š°ø£©£®
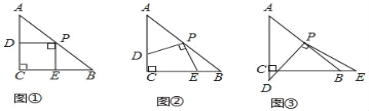
”¾“š°ø”æ£Ø1£©PD=PE,Ö¤Ć÷¼ū½āĪö£»£Ø2£©”÷PCEÄܳÉĪŖµČŃüČż½ĒŠĪ£¬Ö¤Ć÷¼ū½āĪö
”¾½āĪö”æ
£Ø1£©PD=PE£¬ĶعżÖ¤”÷DPC”Õ”÷EPB£¬æÉµĆ½įĀŪ
£Ø2£©·ÖČżÖÖĒéæöĢÖĀŪ¢Łµ±PC£½PE£½![]() Ź±£»¢Śµ±PC£½CE£½
Ź±£»¢Śµ±PC£½CE£½![]() Ź±£»¢Ūµ±PE£½ECŹ±£¬æÉĒó½ā£®
Ź±£»¢Ūµ±PE£½ECŹ±£¬æÉĒó½ā£®
½ā:£Ø1£©PD=PE£¬ĄķÓÉČēĻĀ£ŗ
µ±DŌŚACÉĻŹ±£¬Į¬½ÓPC£¬

ŅņĪŖ”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬PŹĒABµÄÖŠµć£¬
”ąCP=PB£¬CP”ĶAB£¬”ĻACP=![]() ”ĻACB=45”ć£®
”ĻACB=45”ć£®
”ą”ĻACP=”ĻB=45”ć£®
Ó֔ߔĻDPC+”ĻCPE=”ĻBPE+”ĻCPE£¬
”ą”ĻDPC=”ĻBPE£®
”ą”÷PCD”Õ”÷PBE£®
”ąPD=PE£»
µ±DŌŚACÉĻŹ±£¬Į¬½ÓPC£¬

ŅņĪŖ”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬PŹĒABµÄÖŠµć£¬
”ąCP=PB£¬CP”ĶAB£¬”ĻACP=![]() ”ĻACB=45”ć£®
”ĻACB=45”ć£®
”ą”ĻACP=”ĻCBP=45”ć£®
”ą”ĻPCD=”ĻPBE=135”ć£®
Ó֔ߔĻDPC+”ĻDPB=”ĻDPB+”ĻBPE£¬
”ą”ĻDPC=”ĻBPE£®
”ą”÷PCD”Õ”÷PBE£®
”ąPD=PE
×ŪÉĻĖłŹö£ŗPD=PE£»
£Ø2£©”÷PBEŹĒµČŃüČż½ĒŠĪ£¬ĄķÓÉČēĻĀ£ŗ
”ßAC£½BC£½2£¬”ĻC£½90”ć
”ąAB£½2![]()
”ąAP£½BP£½CP£½![]()
”÷PCEŹĒµČŃüČż½ĒŠĪ
µ±PC£½PE£½![]() Ź±£¬¼“B£¬EÖŲŗĻ£¬BE£½0
Ź±£¬¼“B£¬EÖŲŗĻ£¬BE£½0
µ±PC£½CE£½![]() Ź±£¬ĒŅEŌŚĻ߶ĪBCÉĻ£¬ŌņBE£½2©
Ź±£¬ĒŅEŌŚĻ߶ĪBCÉĻ£¬ŌņBE£½2©![]()
µ±PC£½CE£½![]() Ź±£¬ĒŅEŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻ£¬ŌņBE£½2+
Ź±£¬ĒŅEŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻ£¬ŌņBE£½2+![]()
µ±PE£½EC£¬ĒŅ”ĻPCB£½45”ć
”ą”ĻPEC£½90”ć
”ąEC£½1
”ąBE£½1



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔ӱŗĶŠ”ĮĮÉĻɽÓĪĶę£¬Š”Ó±³Ė×ųĄĀ³µ£¬Š”ĮĮ²½ŠŠ£¬Į½ČĖĻąŌ¼ŌŚÉ½¶„µÄĄĀ³µÖÕµć»įŗĻ.ŅŃÖŖŠ”ĮĮŠŠ×ßµ½ĄĀ³µÖÕµćµÄĀ·³ĢŹĒĄĀ³µµ½É½¶„µÄĻßĀ·³¤µÄ2±¶£¬Š”Ó±ŌŚŠ”ĮĮ³ö·¢ŗó50·Ö²Å³ĖÉĻĄĀ³µ£¬ĄĀ³µµÄĘ½¾łĖŁ¶ČĪŖ180Ć×/·Ö£¬É芔ĮĮ³ö·¢x·ÖŗóŠŠ×ßµÄĀ·³ĢĪŖyĆ×£®Ķ¼ÖŠµÄÕŪĻß±ķŹ¾Š”ĮĮŌŚÕūøöŠŠ×ß¹ż³ĢÖŠyĖęxµÄ±ä»Æ¹ŲĻµ.
£Ø1)Š”ĮĮŠŠ×ßµÄ×ÜĀ·³ĢŹĒ_________Ć×£¬ĖūĶ¾ÖŠŠŻĻ¢ĮĖ___________·Ö£»
£Ø2£©·Ö±šĒó³öŠ”ĮĮŌŚŠŻĻ¢Ē°ŗĶŠŻĻ¢ŗóĖł×ßµÄĀ·³Ģ¶ĪÉĻµÄ²½ŠŠĖŁ¶Č£»
£Ø3£©µ±Š”Ó±µ½“ļĄĀ³µÖÕµćŹ±£¬Š”ĮĮĄėĄĀ³µÖÕµćµÄĀ·³ĢŹĒ¶ąÉŁ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
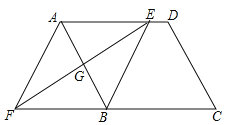
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬±ßABµÄ“¹Ö±Ę½·ÖĻß½»ADÓŚµćE£¬½»CBµÄŃÓ³¤ĻßÓŚµćF£¬Į¬½ÓAF£¬BE£®
£Ø1£©ĒóÖ¤£ŗ”÷AGE”Õ”÷BGF£»
£Ø2£©ŹŌÅŠ¶ĻĖıߊĪAFBEµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
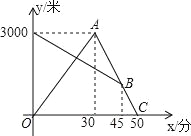
”¾ĢāÄæ”æijĢģŌē³æ£¬ÕÅĒæ“Ó¼ŅÅܲ½Č„ĢåÓż¶ĶĮ¶£¬Ķ¬Ź±ĀčĀč“ÓĢåÓż³”³æĮ·½įŹų»Ų¼Ņ£¬Ķ¾ÖŠĮ½ČĖĻąÓö£¬ÕÅĒæÅܵ½ĢåÓż³”ŗó·¢ĻÖŅŖĻĀÓź£¬Į¢¼“°“ŌĀ··µ»Ų£¬Óöµ½ĀčĀčŗóĮ½ČĖŅ»Ęš»Ųµ½¼Ņ£ØÕÅĒæŗĶĀčĀčŹ¼ÖÕŌŚĶ¬Ņ»Ģõ±ŹÖ±µÄ¹«Ā·ÉĻŠŠ×ߣ©£®ČēĶ¼ŹĒĮ½ČĖĄė¼ŅµÄ¾ąĄėy£ØĆ×£©ÓėÕÅĒæ³ö·¢µÄŹ±¼äx£Ø·Ö£©Ö®¼äµÄŗÆŹżĶ¼Ļó£¬øł¾ŻĶ¼ĻóŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóÕÅĒæ·µ»ŲŹ±µÄĖŁ¶Č£»
£Ø2£©ĀčĀč±Č°“ŌĖŁ·µ»ŲĢįĒ°¶ąÉŁ·ÖÖÓµ½¼Ņ£æ
£Ø3£©ĒėÖ±½ÓŠ“³öÕÅĒæÓėĀčĀčŗĪŹ±Ļą¾ą1000Ć×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĖıߊĪ![]() £¬
£¬![]() £¬µć
£¬µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻŌĖ¶Æ(µć
ÉĻŌĖ¶Æ(µć![]() ŗĶµć
ŗĶµć![]() £¬
£¬![]() ²»ÖŲŗĻ£¬µć
²»ÖŲŗĻ£¬µć![]() £¬
£¬![]() £¬
£¬![]() ²»ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ)£¬Čō¼Ē
²»ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ)£¬Čō¼Ē![]() £¬
£¬![]() £¬
£¬![]() ·Ö±šĪŖ
·Ö±šĪŖ![]() £¬
£¬![]() £¬
£¬![]() .
.
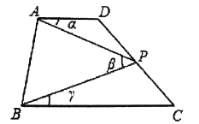
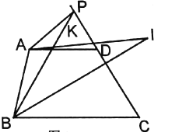
Ķ¼1 Ķ¼2 Ķ¼3
(1)ČēĶ¼1£¬µ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() ÉĻŌĖ¶ÆŹ±£¬Š“³ö
ÉĻŌĖ¶ÆŹ±£¬Š“³ö![]() £¬
£¬![]() £¬
£¬![]() Ö®¼äµÄ¹ŲĻµ£¬²¢Ėµ³öĄķÓÉ£»
Ö®¼äµÄ¹ŲĻµ£¬²¢Ėµ³öĄķÓÉ£»
(2)ČēĶ¼2£¬Čē¹ūµć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() µÄŃÓ³¤ĻßÉĻŌĖ¶Æ£¬Ģ½¾æ
µÄŃÓ³¤ĻßÉĻŌĖ¶Æ£¬Ģ½¾æ![]() £¬
£¬![]() £¬
£¬![]() Ö®¼äµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ.
Ö®¼äµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ.
(3)ČēĶ¼3£¬![]() Ę½·Ö
Ę½·Ö![]() £¬
£¬![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬½»
£¬½»![]() ÓŚµć
ÓŚµć![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() µÄ¶ČŹż.
µÄ¶ČŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
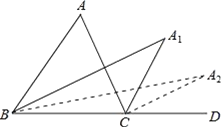
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻA=m”ć£¬”ĻABCŗĶ”ĻACDµÄĘ½·ÖĻß½»ÓŚµćA1£¬µĆ”ĻA1£»”ĻA1BCŗĶ”ĻA1CDµÄĘ½·ÖĻß½»ÓŚµćA2£¬µĆ”ĻA2£»””ĻA2015BCŗĶ”ĻA20l5CDµÄĘ½·ÖĻß½»ÓŚµćA2016£¬Ōņ”ĻA2016=__£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø![]() ·Ö£©ČēĶ¼£¬¹ÜÖŠ·ÅÖĆ×ÅČżøłĶ¬ŃłµÄÉž×Ó
·Ö£©ČēĶ¼£¬¹ÜÖŠ·ÅÖĆ×ÅČżøłĶ¬ŃłµÄÉž×Ó![]() £¬
£¬ ![]() £¬
£¬ ![]() £®
£®
£Ø![]() £©Š”Ć÷“Ó
£©Š”Ć÷“Ó![]() ÕāČżøłÉž×ÓÖŠĖ껜єŅ»øł£¬Ē”ŗĆє֊ɞ×Ó
ÕāČżøłÉž×ÓÖŠĖ껜єŅ»øł£¬Ē”ŗĆє֊ɞ×Ó![]() µÄøÅĀŹŹĒ__________£®
µÄøÅĀŹŹĒ__________£®
£Ø![]() £©Š”Ć÷ĻČ“Ó×ó¶Ė
£©Š”Ć÷ĻČ“Ó×ó¶Ė![]() £¬
£¬ ![]() £¬
£¬ ![]() ČżøöÉžĶ·ÖŠĖ껜єĮ½øö“ņŅ»øö½į£¬ŌŁ“ÓÓŅ¶Ė
ČżøöÉžĶ·ÖŠĖ껜єĮ½øö“ņŅ»øö½į£¬ŌŁ“ÓÓŅ¶Ė![]() £¬
£¬ ![]() £¬
£¬ ![]() ČżøöÉžĶ·ÖŠĖ껜єĮ½øö“ņŅ»øö½į£¬ĒóÕāČżøłÉž×ÓÄÜĮ¬½į³ÉŅ»øł³¤ÉžµÄøÅĀŹ£®
ČżøöÉžĶ·ÖŠĖ껜єĮ½øö“ņŅ»øö½į£¬ĒóÕāČżøłÉž×ÓÄÜĮ¬½į³ÉŅ»øł³¤ÉžµÄøÅĀŹ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
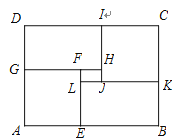
”¾ĢāÄæ”æŌŚ¾ŲŠĪABCDÖŠ£¬AB=8£¬BC=6£¬½«¾ŲŠĪ°“Ķ¼Ź¾·½Ź½½ųŠŠ·Öøī£¬ĘäÖŠÕż·½ŠĪAEFGÓėÕż·½ŠĪJKCIČ«µČ£¬¾ŲŠĪGHIDÓė¾ŲŠĪEBKLČ«µČ£®
£Ø1£©µ±¾ŲŠĪLJHFµÄĆ껿ĪŖ![]() Ź±£¬ĒóAGµÄ³¤£»
Ź±£¬ĒóAGµÄ³¤£»
£Ø2£©µ±AGĪŖŗĪÖµŹ±£¬¾ŲŠĪLJHFµÄĆ껿×ī“ó£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ¼ÓĒæѧɜæĪĶāŌĶĮ£¬æŖĄ«ŹÓŅ°£¬Ä³Š£æŖÕ¹ĮĖ”°ŹéĻćŠ£Ō°£¬ĖŠ¶Į¾µä”±»ī¶Æ£¬Ń§Ļ°Ė껜³é²éĮĖ²æ·Öѧɜ£¬¶ŌĖūĆĒĆæĢģµÄæĪĶāŌĶĮŹ±¼ä½ųŠŠµ÷²é£¬²¢½«µ÷²éĶ³¼ĘµÄ½į¹ū·ÖĪŖĖÄĄą£ŗĆæĢģĖŠ¶ĮŹ±¼ät”Ü20·ÖÖÓµÄѧɜ¼ĒĪŖAĄą£¬20·ÖÖÓ£¼t”Ü40·ÖÖÓ¼ĒĪŖBĄą£¬40·ÖÖÓ£¼t”Ü60·ÖÖÓ¼ĒĪŖCĄą£¬t£¾60·ÖÖÓ¼ĒĪŖDĄą£¬ŹÕ¼ÆµÄŹż¾Ż»ęÖĘČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ

£Ø1£©Õā“Ī¹²³éČ”ĮĖ”” ””Ćūѧɜ½ųŠŠµ÷²éĶ³¼Ę£¬ÉČŠĪĶ³¼ĘĶ¼ÖŠDĄąĖł¶ŌÓ¦µÄÉČŠĪŌ²ŠÄ½Ē“óŠ”ĪŖ”” ””£»
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©Čē¹ūøĆŠ£¹²ÓŠ2000Ćūѧɜ£¬ĒėÄć¹Ą¼ĘøĆŠ£CĄąŃ§ÉśŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com