
分析 (1)运用不等式的性质和因式分解,由$\frac{{a}^{2}+b}{{b}^{2}+a}$≥1可推出a≥b,然后用反证法证明a=b不成立,从而解决问题;
(2)设$\frac{{a}^{2}+b}{{b}^{2}+a}$=k(其中k>1,k为正整数),则有a2+b=k(b2+a)=kp2,与条件“b2+a=p2”结合,可得p2=$\frac{(a-b)(a+b-1)}{k-1}$.若$\frac{a-b}{k-1}$为正整数,则$\frac{a-b}{k-1}$与a+b-1中有一个是1,另一个是p2,或两个都是p;若$\frac{a+b-1}{k-1}$是正整数,则a-b与$\frac{a+b-1}{k-1}$中有一个是1,另一个是p2,或两个都是p.只需通过分类讨论就可解决问题;
(3)由(2)可知,只有当$\frac{a+b-1}{k-1}$=a-b=p时,存在正整数a、b及质数p,使得条件成立,此时(a-b)2=p2=b2+a,整理得a=2b+1,从而得到k=$\frac{{a}^{2}+b}{{b}^{2}+a}$=4-$\frac{3}{b+1}$.由k是大于1的正整数可得$\frac{3}{b+1}$是小于3的正整数,从而求出b,就可得到a.
解答 解:(1)∵a,b是两个不相等的正整数,
∴a2+b,b2+a都是正整数,a+b-1>0.
∵$\frac{{a}^{2}+b}{{b}^{2}+a}$是整数,
∴$\frac{{a}^{2}+b}{{b}^{2}+a}$≥1,
∴a2+b≥b2+a,
∴a2+b-b2-a=(a+b)(a-b)-(a-b)=(a-b)(a+b-1)≥0,
∴a-b≥0即a≥b.
假设a=b,
则有p2=b2+a=a2+a=a(a+1).
∵a与a+1连续整数,
∴p2是偶数,
∵P为质数,
∴p=2,
∴b2+a=4,
∴b=1,a=3,
∴$\frac{{a}^{2}+b}{{b}^{2}+a}$=$\frac{10}{4}$=$\frac{5}{2}$,
与条件“$\frac{{a}^{2}+b}{{b}^{2}+a}$是整数”矛盾,
∴a>b;
(2)设$\frac{{a}^{2}+b}{{b}^{2}+a}$=k(其中k>1,k为正整数),
则有a2+b=k(b2+a)=kp2,
∴(k-1)p2=kp2-p2=a2+b-b2-a=(a-b)(a+b-1),
∴p2=$\frac{(a-b)(a+b-1)}{k-1}$.
∵P是质数,
∴p2=1×p2=p×p.
①$\frac{a-b}{k-1}$=1且a+b-1=p2,
此时a+b-1=p2=b2+a,整理得b2-b+1=0,
方程无解.
②$\frac{a-b}{k-1}$=p2且a+b-1=1,
此时a+b=2,与条件“a、b为不相等的正整数”矛盾;
③$\frac{a-b}{k-1}$=a+b-1=p,
此时(a+b-1)2=p2=b2+a,
∴a=(a+b-1)2-b2=(a+2b-1)(a-1),
∴a+2b-1=$\frac{a}{a-1}$=1+$\frac{1}{a-1}$.
∵a+2b-1为整数,
∴$\frac{1}{a-1}$也是整数,
∴正整数a=2.
∵a>b,
∴正整数b=1,
∴p=a+b-1=2,
∴$\frac{1}{k-1}$=2,
∴k=$\frac{3}{2}$,与k为正整数矛盾;
④$\frac{a+b-1}{k-1}$=1且a-b=p2,
此时a-b=p2=b2+a,
整理得b2+b=0,
解得b1=0,b2=-1,
与b为正整数矛盾;
⑤$\frac{a+b-1}{k-1}$=p2且a-b=1,
此时a=b+1,
k=$\frac{{a}^{2}+b}{{b}^{2}+a}$=$\frac{(b+1)^{2}+b}{{b}^{2}+b+1}$
=$\frac{{b}^{2}+3b+1}{{b}^{2}+b+1}$
=1+$\frac{2b}{{b}^{2}+b+1}$
∵b2+b+1-2b=b2-b+1=(b-$\frac{1}{2}$)2+$\frac{3}{4}$>0,
∴b2+b+1>2b>0,
∴$\frac{2b}{{b}^{2}+b+1}$<1,
∴k<2,
与“k是大于1的正整数”矛盾;
⑥$\frac{a+b-1}{k-1}$=a-b=p,
此时(a-b)2=p2=b2+a,
整理得a=2b+1,
则k=$\frac{{a}^{2}+b}{{b}^{2}+a}$=$\frac{(2b+1)^{2}+b}{{b}^{2}+2b+1}$=$\frac{4{b}^{2}+5b+1}{{b}^{2}+2b+1}$
=$\frac{(4b+1)(b+1)}{(b+1)^{2}}$=$\frac{4b+1}{b+1}$=4-$\frac{3}{b+1}$.
∵k是大于1的正整数,
∴$\frac{3}{b+1}$是小于3的正整数,
∴整数b+1=3,
∴b=2,
∴a=2b+1=5,
∴p=a-b=3.
综上所述:p=3;
(3)由(2)可知,
只有当$\frac{a+b-1}{k-1}$=a-b=p时,存在正整数a、b及质数p,使得条件成立,
此时(a-b)2=p2=b2+a,整理得a=2b+1,
则k=$\frac{{a}^{2}+b}{{b}^{2}+a}$=$\frac{(2b+1)^{2}+b}{{b}^{2}+2b+1}$=$\frac{4{b}^{2}+5b+1}{{b}^{2}+2b+1}$
=$\frac{(4b+1)(b+1)}{(b+1)^{2}}$=$\frac{4b+1}{b+1}$=4-$\frac{3}{b+1}$.
∵k是大于1的正整数,
∴$\frac{3}{b+1}$是小于3的正整数,
∴整数b+1=3,
∴b=2,
∴a=2b+1=5.
点评 本题考查了质数与合数、质因数的分解、因式分解、分式的分解等知识,难度比较大,在解决问题的过程中用到了分类讨论、转化(将一个分式转化为一个整数与一个分子是整数的简单分式的和)、反证法等重要的数学思想方法,应学会使用.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
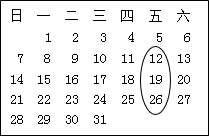 如图,是某月份的日历表,如图那样,用一个圈竖着圈住3个数,当你任意圈出一竖列上相邻的三个数时,请你运用方程思想来研究,发现这三个数的和不可能是( )
如图,是某月份的日历表,如图那样,用一个圈竖着圈住3个数,当你任意圈出一竖列上相邻的三个数时,请你运用方程思想来研究,发现这三个数的和不可能是( )| A. | 72 | B. | 60 | C. | 27 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
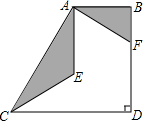 在图中的直角梯形中,AC=CD=2AB,∠ACE=∠ECD,△EAF=2∠CAE=2∠FAB,若梯形的面积为60,则阴影部分的面积等于20.
在图中的直角梯形中,AC=CD=2AB,∠ACE=∠ECD,△EAF=2∠CAE=2∠FAB,若梯形的面积为60,则阴影部分的面积等于20.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<p<q<n | B. | p<m<n<q | C. | m<p<n<q | D. | p<m<q<n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,正方形ABCD的边长为4cm,E,F分别是BC,DC边上的动点,E,F同时从点C以1cm/s的速度分别向点B、点D移动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y.
如图所示,正方形ABCD的边长为4cm,E,F分别是BC,DC边上的动点,E,F同时从点C以1cm/s的速度分别向点B、点D移动,当点E与点B重合时,运动停止,设运动时间为x(s),运动过程中△AEF的面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com