【题目】某地区经过三年的新农村建设，年经济收入实现了翻两番（即是原来的22倍）．为了更好地了解该地区的经济收入变化情况，统计了该地区新农村建设前后的年经济收入构成结构如图，则下列结论中不正确的是（ ）
A.新农村建设后，种植收入减少了
B.新农村建设后，养殖收入实现了翻两番
C.新农村建设后，第三产业收入比新农村建设前的年经济收入还多
D.新农村建设后，第三产业收入与养殖收入之和超过了年经济收入的一半
【答案】A
【解析】
设建设前经济收入为a，建设后经济收入为4a．通过选项逐一分析新农村建设前后，经济收入情况，利用数据推出结果．
解：设建设前经济收入为a，建设后经济收入为4a．
A、建设后，种植收入为30%×4a＝120%a，
建设前，种植收入为55%a，
故新农村建设后，种植收入增加了，故A项符合题意；
B、建设后，养殖收入为30%×4a＝120%a，
建设前，养殖收入为30%a，
故120%a÷30%a＝4，故B项不符合题意；
C、建设后，第三产业收入为32%×4a＝128%a，故第三产业收入比新农村建设前的年经济收入还多，故C项不符合题意；
D、建设后，养殖收入与第三产业收入总和为（30%+32%）×4a＝248%a，
经济收入的一半为2a，
故248%a＞2a，故D项不符合题意．
故选：A．
目标测试系列答案科目：初中数学 来源： 题型：
【题目】全球已经进入大数据时代，大数据（bigdata）是指数据规模巨大，类型多样且信息传播速度快的数据库体系．大数据在推动经济发展，改善公共服务等方面日益显示出巨大的价值．为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是根据调查结果绘制出不完整的两个统计图表：
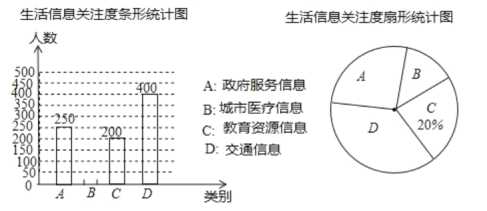
请根据图中提供的信息，解答下列问题：
（1）本次参与调查的人数是________，扇形统计图中
部分的圆心角的度数是________，并补全条形统计图；
（2）这次调查的市民最关心的四类生活信息的众数是________类；
（3）若我市现有常住人口约600万，请你估计最关心“城市医疗信息”的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系
中的任意一点
，给出如下定义：经过点且平行于两坐标轴夹角平分线的直线，叫做点的“特征线”．例如：点
的特征线是
和
．
（1）若点
的其中一条特征线是
，则在
、
、
三个点中，可能是点的点有_______；
（2）已知点
的平行于第二、四象限夹角平分线的特征线与
轴相交于点
，直线
经过点，且与轴交于点
．使
的面积不小于6，求
的取值范围；
（3）已知点
，
，且
的半径为1．当与点
的特征线存在交点时，直接写出
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一笔总额为
元的奖金，分为一等奖、二等奖和三等奖，奖金金额均为整数，每个一等奖的奖金是每个二等奖奖金的两倍，每个二等奖的奖金是每个三等奖奖金的两倍，若把这笔奖金发给
个人，评一、二、三等奖的人数分别为
，且
，那么三等奖的奖金金额是_______元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，四边形ABCD为矩形，曲线L经过点D．点Q是四边形ABCD内一定点，点P是线段AB上一动点，作PM⊥AB交曲线L于点M，连接QM．
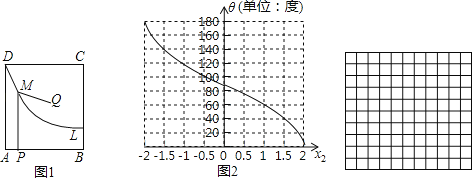
小东同学发现：在点P由A运动到B的过程中，对于x1＝AP的每一个确定的值，θ＝∠QMP都有唯一确定的值与其对应，x1与θ的对应关系如表所示：
x1＝AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ＝∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时，发现了另外一个函数：对于自变量x2在﹣2≤x2≤2范围内的每一个值，都有唯一确定的角度θ与之对应，x2与θ的对应关系如图2所示：
根据以上材料，回答问题：
（1）表格中α的值为 ．
（2）如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等，可以在两个变量x1与x2之间建立函数关系．
①在这个函数关系中，自变量是 ，因变量是 ；（分别填入x1和x2）
②请在网格中建立平面直角坐标系，并画出这个函数的图象；
③根据画出的函数图象，当AP＝3.5时，x2的值约为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
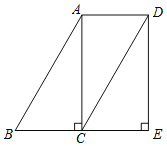
【题目】如图，在ABCD中，∠ACB＝90°，过点D作DE⊥BC交BC的延长线于点E．
（1）求证：四边形ACED是矩形；
（2）连接AE交CD于点F，连接BF．若∠ABC＝60°，CE＝2，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
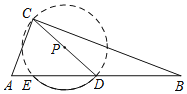
【题目】在△ABC中，以AB边上的中线CD为直径作圆，如果与边AB有交点E（不与点D重合），那么称
为△ABC的C﹣中线弧．例如，如图中是△ABC的C﹣中线弧．在平面直角坐标系xOy中，已知△ABC存在C﹣中线弧，其中点A与坐标原点O重合，点B的坐标为（2t，0）（t＞0）．
（1）当t＝2时，
①在点C1（﹣3，2），C2（0，2
），C3（2，4），C4（4，2）中，满足条件的点C是 ；
②若在直线y＝kx（k＞0）上存在点P是△ABC的C﹣中线弧所在圆的圆心，其中CD＝4，求k的取值范围；
（2）若△ABC的C﹣中线弧所在圆的圆心为定点P（2，2），直接写出t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，抛物线
，与x轴交于A、B两点(点A在点B的左侧)．
（1）求点A和点B的坐标；
（2）若点P（m，n）是抛物线上的一点，过点P作x轴的垂线，垂足为点D．
①在
的条件下，当
时，n的取值范围是
，求抛物线的表达式；
②若D点坐标（4，0），当
时，求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
