
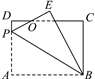
【题目】如图,长方形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长.
【答案】AP=4.8.
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
如图所示,设BE与CD交于点G,

∵四边形ABCD是长方形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.,
根据题意,得△ABP≌△EBP,
∴AP=EP,∠A=∠E=90°,AB=EB=8.
在△ODP和△OEG中,
∵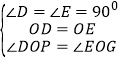 ,
,
∴△ODP≌△OEG,
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理,得BC2+CG2=BG2,
即62+(8-x)2=(2+x)2,
解得x=4.8,
∴AP=4.8.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】本学期第三周周末,七年级27班在人美心善的范老师的带领下开展了大型“绿水青山都是金山银山”的植树活动.全班一起种植许愿树和发财树.已知购买1棵许愿树和2棵发财树需要42元,购买2棵许愿树和1棵发财树需要48元.
(1)你来算一算许愿树、发财树每棵各多少钱?
(2)范老师传达最高指示:全班种植许原树和发财树共20棵,且许愿树的数量不少于发财树的数量,但由于班费资金紧张,范老师还要求两种树的总成本不得高于312元.聪明的同学们,你们知道共有哪几种种植方案吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( ) 
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售甲、乙两种商品,现有如下信息:
信息1:甲、乙两种进货单价之和是3元;
信息2:甲商品零售价比进货价多1元,乙商品零售价比进货价的2倍少1元;
信息3:按零售单价购买甲商品4件和乙商品3件,共付了17元.
请根据以上信息,求甲乙两种商品的零售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C 为线段 AD 上一点,B 为 CD 的中点,AD=13cm,BD=3cm.
(1)图中共有 条线段;
(2)求 AC 的长;
(3)若点 E 在线段 AD 上,且 BE=2cm,求 AE 的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上一动点![]() 从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的
从原点出发,在数轴上进行往返运动,运动情况如下表(注:表格中的![]() 表示2到4之间的数).
表示2到4之间的数).
![]()
运动次数 | 运动方向 | 运动路程 | 数轴上对应的数 |
第1次 | _________ | 3 | -3 |
第2次 | 左 |
| _________ |
第3次 | _________ | _________ |
|
回答下列问题:
(1)完成表格;
(2)已知第4次运动的路程为![]() .
.
①此时数轴上对应的数是_________;
②若第4次运动后点![]() 恰好回到原点,则这4次运动的总路程是多少?
恰好回到原点,则这4次运动的总路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= ![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示). 
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下![]() 两个情境:
两个情境:

情境![]() :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
情境![]() :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
(1)情境![]() ,
, ![]() 所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).
(2)请你为剩下的函数图象写出一个适合的情境.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com