
| A. | 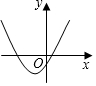 | B. | 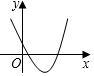 | C. | 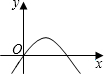 | D. | 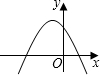 |
分析 根据a的符号确定抛物线的开口方向,根据c的符号确定抛物线与y轴的交点.
解答 解:∵二次函数y=ax2+bx+c,a>0,c<0,
∴抛物线开口向上,与y轴交点在x轴的下方,
故选A.
点评 本题考查的是二次函数图象与系数的关系,对于二次函数y=ax2+bx+c(a≠0)来说,①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;|a|还可以决定开口大小,|a|越大开口就越小;②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右(简称:左同右异);③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);④抛物线与x轴交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:解答题
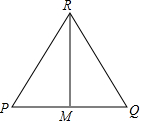 已知:如图,△RPQ中,RP=RQ,M为PQ的中点.
已知:如图,△RPQ中,RP=RQ,M为PQ的中点.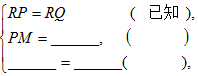
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
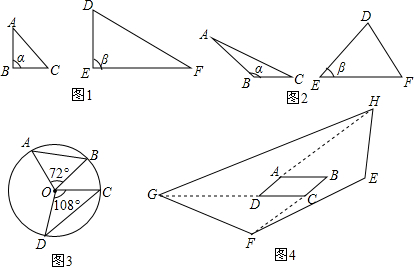
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
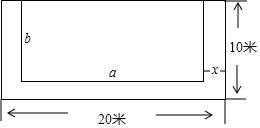 如图,有一块长为20米,宽10米的长方形土地,现将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:
如图,有一块长为20米,宽10米的长方形土地,现将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com