
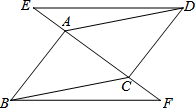
 如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.
如图,已知点A、C在EF上,AD∥BC,DE∥BF,AE=CF.分析 (1)证△ADE≌△CBF,得AD=CB,从而得出四边形ABCD是平行四边形;
(2)由全等三角形的性质和平行四边形的性质容易得出结果.
解答 (1)证明:∵AD∥BC,DE∥BF,
∴∠E=∠F,∠DAC=∠BCA,
∴∠DAE=∠BCF,
在△ADE和△CBF中,$\left\{\begin{array}{l}{∠E=∠F}&{\;}\\{AE=CF}&{\;}\\{∠DAE=∠BCF}&{\;}\end{array}\right.$,
∴△ADE≌△CBF(ASA),
∴AD=CB,
∴四边形ABCD是平行四边形;
(2)解:AD=BC、EC=AF、ED=BF、AB=DC;理由如下:
∵△ADE≌△CBF,
∴AD=BC,ED=BF,
∵AE=CF,
∴EC=AF,
∵四边形ABCD是平行四边形,
∴AB=DC.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
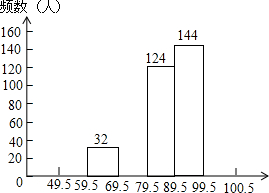 某市九年级有15000名学生参加学业水品测试,为了了解本次测试的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
某市九年级有15000名学生参加学业水品测试,为了了解本次测试的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:| 分 组 | 频 数 | 频 率 |
| 49.5~59.5 | 20 | 0.05 |
| 59.5~69.5 | 32 | 0.08 |
| 69.5~79.5 | 80 | 0.20 |
| 79.5~89.5 | 124 | 0.31 |
| 89.5~100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com