练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    把抛物线先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为（  ）。

    A. B.

    C. D.

    B 【解析】试题分析：抛物线y＝x2－1的顶点坐标为（0，－1）， ∵向右平移一个单位，再向下平移2个单位， ∴平移后的抛物线的顶点坐标为（1，－3）， ∴得到的抛物线的解析式为y＝ (x－1)2－3． 故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：单选题

    不能判定四边形ABCD为平行四边形的题设是（　　）

    A. AB=CD，AB∥CD B. ∠A=∠C，∠B=∠D

    C. AB=AD，BC=CD D. AB=CD，AD=BC

    C 【解析】A.∵AB=CD，AB∥CD， ∴四边形ABCD为平行四边形(一组对边平行且相等的四边形是平行四边形)；股本选项能判定四边形ABCD为平行四边形； B.∵∠A=∠C，∠B=∠D， ∴四边形ABCD为平行四边形(两组对角分别相等的四边形是平行四边形)；股本选项能判定四边形ABCD为平行四边形； C. 由AB=AD，BC=CD，不能判定四边形ABCD为平行...

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：单选题

    下列运算正确的是(　 　)

    A. B. C. D.

    C 【解析】根据算术平方根的定义，易得C.

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为_____mm．

    8 【解析】试题分析：先求出钢珠的半径及OD=3mm，连接OA，过点O作OD⊥AB于点D，则AB=2AD，在Rt△AOD中利用勾股定理即可求出AD4mm，进而得出AB=8mm．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    二次函数的图象如图，则一次函数y=mx+n的图象经过

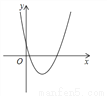
    A. 第一、二、三象限 B. 第一、二、四象限

    C. 第二、三、四象限 D. 第一、三、四象限

    C 【解析】试题分析：∵抛物线的顶点（－m，n）在第四象限， ∴－m＞0，n＜0， ∴m＜0， ∴一次函数y＝mx＋n的图象经过二、三、四象限， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：解答题

    已知一次函数y=kx+b的图象经过点A（-4，0），B（2，6）两点．

    （1）求一次函数y=kx+b的表达式；

    （2）在直角坐标系中，画出这个函数的图象；

    （3）求这个一次函数与坐标轴围成的三角形面积．

    （1）； （2）函数图像如图： （3）8 【解析】 试题分析：（1）由图象经过两点A（-4，0）、B（2，6）根据待定系数法即得结果； （2）根据两点法即可确定函数的图象； （3）求出图象与x轴及y轴的交点坐标，然后根据直角三角形的面积公式求解即可． （1）∵一次函数y=kx+b的图象经过两点A（-4，0）、B（2，6） ，解得， ∴函数解析式...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：填空题

    函数y=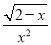的自变量x的取值范围是__________

    x≤2且x≠0 【解析】根据分式有意义的条件和二次根式有意义的条件，可知x≠0,2-x≥0，解得x≤2且x≠0. 故答案为：x≤2且x≠0.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：解答题

    如图，在△ABC中，AD是BC边上的高，tanB＝cos∠DAC.

    （1）求证：AC＝BD；

    （2）若sin C＝，BC＝12，求△ABC的面积．

    （1）证明见解析；（2）△ABC的面积为48. 【解析】(1)∵AD是BC上的高，∴AD⊥BC． ∴∠ADB=90°，∠ADC=90°． …………………………………………1分 在Rt△ABD和Rt△ADC中， ∵=， =…………………………………………3分 又已知 ∴=．∴AC=BD． ………………………………4分 (2)在Rt△ADC中， ，故可设AD=...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型：解答题

    根据如图所给出的几何体从三个方向看得到的形状图，试确定几何体中小正方体的数目的范围．

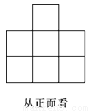
    最多需要11个，最少需要9个小正方体． 【解析】试题分析：根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，进而得出答案． 试题解析：【解析】 根据题意，构成几何体所需正方体最多情况如图（1）所示，构成几何体所需正方体最少情况如图（2）所示： 所以最多需要11个，最少需要9个小正方体．

    查看答案和解析>>

    同步练习册答案