
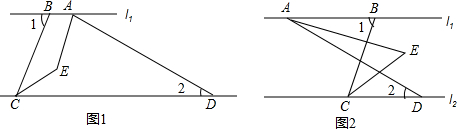
分析 (1)利用平行线的性质结合角平分线的性质得出∠BAE以及∠AEF的度数即可得出答案;
(2)利用平行线的性质结合角平分线的性质得出∠ECD以及∠AEF的度数即可得出答案.
解答 解:(1)如图1,过点E作EF∥l1,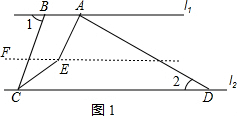
∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠α,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD=$\frac{1}{2}$×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
∵l1∥l2,
∴∠BAD+∠2=180°,
∵∠2=30°,
∴∠BAD=150°,
∵AE平分∠BAD,
∴∠BAE=$\frac{1}{2}$×150°=75°,
∵EF∥l1,
∴∠BAE+∠AEF=180°,
∴∠AEF=105°,
∴∠AEC=105°+35°=140°;
(2)如图2,过点E作EF∥l1,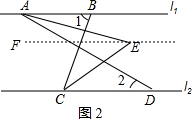
∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠1,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD=$\frac{1}{2}$×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
同理可求∠AEF=15°,
∴∠AEC=∠AEF+∠CEF=50°.
点评 此题主要考查了平移的性质以及角平分线的性质、平行线的性质等知识,正确应用平行线的性质得出各角之间关系是解题关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
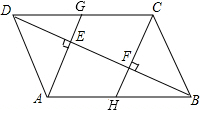 如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H.
如图,在?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于点G、H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
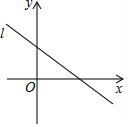 如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )
如图,直线l:y=-$\frac{3}{5}$x+3与直线x=a(a为常数)的交点在第四象限,则关于a的取值范围在数轴上表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=t-0.5 | B. | y=t-0.6 | C. | y=3.4t-7.8 | D. | y=3.4t-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1×104 | B. | 1×105 | C. | 1×106 | D. | 1×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
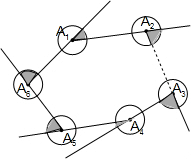 如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )| A. | πcm2 | B. | 2πcm2 | C. | 2016πcm2 | D. | 2017πcm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com