
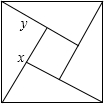
 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( )| A. | x2+y2=49 | B. | x-y=2 | C. | 2xy+4=49 | D. | x+y=9 |
分析 由题意 $\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49①}\\{(x-y)^{2}=4②}\end{array}\right.$,①-②可得2xy=45记为③,①+③得到(x+y)2=94由此即可判断.
解答 解:由题意 $\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49①}\\{(x-y)^{2}=4②}\end{array}\right.$,
①-②可得2xy=45 ③,
∴2xy+4=49,
①+③得x2+2xy+y2=94,
∴x+y=$\sqrt{94}$,
∴①②③正确,④错误.
故选D.
点评 本题考查勾股定理,二元二次方程组等知识,解题的关键学会利用方程的思想解决问题,学会整体恒等变形的思想,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
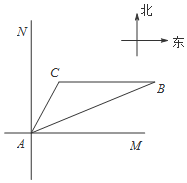 如图所示,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:
如图所示,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{5}{3}$ | C. | -$\frac{5}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
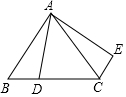 如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )
如图,在等边三角形ABC中,AB=2,动点D从B开始沿BC向点C运动,到达点C后停止运动,将△ABD绕点A旋转后得到△ACE,则下列说法中,正确的是( )| A. | ①③④ | B. | ①②③ | C. | ②③④ | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com