
����Ŀ����ѧ��С���ͬѧһ��������ҵ������һ�ҹ�˾����˾�Ծ�Ӫ��ӯ�������ÿ�µ����һ�����һ��.��1��12�·��У��ù�˾ǰx�����ۼƻ�õ�������y����Ԫ��������ʱ��x���£�֮��������κ�����ϵ.
��1����y��x������ϵʽ.
��2���ù�˾���ĸ��¿�ʼ��Ť��Ϊӯ��������ӯ����? ֱ��д��9�·�һ����������õ�����.
��3����ǰ12 �����У��ĸ��¸ù�˾�������������������Ϊ���٣�
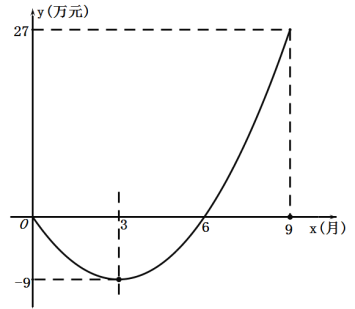
���𰸡���1��![]() ����2����4�·���Ť��Ϊӯ�� 9�·�һ��������Ϊ11��Ԫ ����3��12��17��Ԫ.
����2����4�·���Ť��Ϊӯ�� 9�·�һ��������Ϊ11��Ԫ ����3��12��17��Ԫ.
��������
��1����������������ߵĶ�������Ϊ![]() ����������ߵĶ���ʽ����
����������ߵĶ���ʽ����![]() ���뼴�����
���뼴�����![]() ��ֵ����
��ֵ����![]() ��ֵ���������ߵĶ���ʽ�м���ȷ���������ߵĽ���ʽ��
��ֵ���������ߵĶ���ʽ�м���ȷ���������ߵĽ���ʽ��
��2����ͼ�ɽ����8��9�����·ݵ�������IJΪ9�µ�����
��3������ǰ![]() ����������õ������ȥǰ
����������õ������ȥǰ![]() ����������õ������ɱ�ʾ����
����������õ������ɱ�ʾ����![]() ����������õ�����Ϊ����
����������õ�����Ϊ����![]() ��һ�κ�������Ϊ���������õ�
��һ�κ�������Ϊ���������õ�![]() ȡ���Ϊ12ʱ����
ȡ���Ϊ12ʱ����![]() ���뼴�������������
���뼴�������������
��1������������裺![]() ��
��
�ߵ�![]() ���������ϣ�
���������ϣ�
��![]() ��
��
��ã�![]() ��
��
��![]() ��
��![]() ��
��
��2����![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() ��
��
�൱![]() ʱy��x�����������
ʱy��x�����������
���4�·���Ť��Ϊӯ��
8�·�ǰ��������Ϊ��![]() ��Ԫ,
��Ԫ,
9�·�ǰ��������Ϊ��![]() ��Ԫ,
��Ԫ,
��9�·�һ��������Ϊ��![]() ��Ԫ��
��Ԫ��
��3���赥������ΪW��Ԫ��
������ã�![]() ��
��
�����ã�![]() ��
��
��![]() ��
��
��W��![]() ���������
���������
�൱x��12ʱ����������������Ϊ17��Ԫ


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
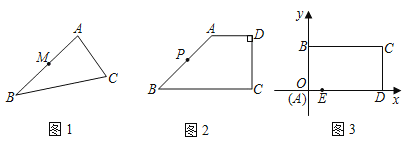
����Ŀ�����һ��ֱ�߰�һ��ƽ��ͼ�ε�����ֳ���ȵ������֣����ǰ�����ֱ�߳�Ϊ���ƽ��ͼ�ε�����ȷ��ߣ�
����̽��
��1����ͼ1����ABC�У���M��AB�ߵ��е㣬�������M����ABC��һ������ȷ��ߣ�
��2����ͼ2�����ı���ABCD�У�AD��BC��CD��AD��AD��2��CD��4��BC��6����P��AB���е㣬��Q��CD�ϣ���̽����CQ�ij�Ϊ����ʱ��ֱ��PQ���ı���ABCD��һ������ȷ��ߣ�
������
��3����ͼ3����ƽ��ֱ������ϵ�У�����ABCD��ij��˾��Ҫ�ィ�Ļ�ʾ��ͼ��A��ԭ���غϣ�D��B�ֱ���x�ᡢy���ϣ�����AB��3��BC��5�������E�ڱ�AD�ϣ���AE��1�����ڱ�BC��AB��CD������������һ�������F��G��H����EF��GH��������ֱ�ĵ�·��·�Ŀ��Ȳ��ƣ������ֳ��Ŀ飬��ÿһ���ڸ���ֲһ�ֻ��ݣ���Ҫ�����ֻ��ݵ���ֲ�����ȣ����������ʱֱ��EF��GH�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
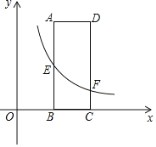
����Ŀ����ͼ������ABCD������AD��AB�ij��ֱ�Ϊ3��8��E��AB���е㣬����������y��![]() ��ͼ����E����CD���ڵ�F��
��ͼ����E����CD���ڵ�F��
��1������C����Ϊ��6��0������m��ֵ��ͼ��D��E�����ֱ�߽���ʽ��
��2����DF��DE��2�����������ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��600��ѧ�����������п�ǰ������һ��ģ�����.���������ȡ����ѧ������������Գɼ���������������ͳ��ͼ.����������Ϣ������������⣺
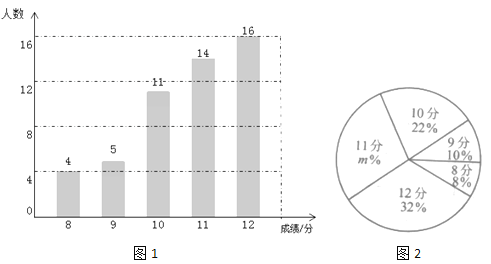
�����γ�ȡ����ѧ������Ϊ ��ͼ2��![]() ��ֵΪ ��
��ֵΪ ��
�����ε����ȡ���������ݵ�ƽ��������������λ����
�������������ݣ����Ƹ�У���꼶ģ������е�12�ֵ�ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ���ABC�У���D��E��F�ֱ���AB��AC��BC�е㣬��M��CB���ӳ����ϣ���DMNΪ�ȱ������Σ���EN����F��.���н��ۣ���EN=MF ��MB=FN ��MP��DP=NP��FP ��MB��BP=PF��FC����ȷ�Ľ����У� ��
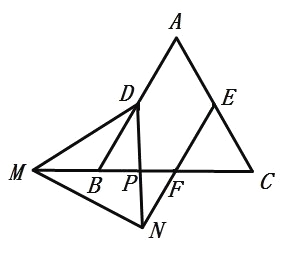
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014����ʡ���������2013������8.9%��2015���2014������9.5%����2013���2015����ʡ��������ֱ�Ϊa��Ԫ��b��Ԫ����a��b֮������Ĺ�ϵʽΪ��������
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O��ԭ���غϣ�����A��C�ֱ���x�ᡢy���ϣ�˫����y��kx��1��k��0��x��0�����AB��BC�ֱ��ڵ�N��F������ON��OF��NF������NOF��45����NF��2�����C������Ϊ_____��
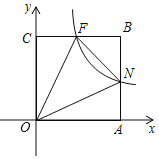
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ¥���������һ��ɽ�£���������һ��ƽ�أ���ͼ��ʾ��BC��AD��BE��AD��б��AB��Ϊ26�ף�б��AB���±�Ϊi��12��5��Ϊ�˼��������ɽ�廬�£����ϰ�ȫ��ѧУ�����Ը�б�½��и��죬��������Ա���⣬���½Dz�����50��ʱ����ȷ��ɽ�岻���£�
��1�������ǰ�¶�������ľ���BE�ij���
��2���������ʱ�����½�A�������¶�B��BC������11��F�㴦��������������ȷ����ȫ�𣿣�tan48.8���1.14��
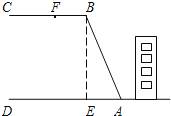
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�AD��BC���ϵĸߣ�
�У�AD��BC���ϵĸߣ�![]() ��
��
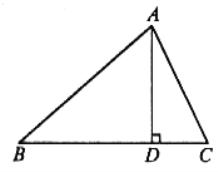
��1����֤��AC��BD
��2����![]() ����AD�ij���
����AD�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com