
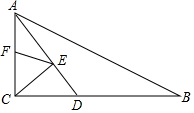
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )| A. | $\frac{40}{3}$ | B. | $\frac{15}{4}$ | C. | $\frac{24}{5}$ | D. | 6 |
分析 依据勾股定理可求得AB的长,然后在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E,先证明C′E=CE,然后可得到CE+EF=C′E+EF,然后依据垂直线段最短可知当点C′F⊥AC时,CE+EF有最小值,最后利用相似三角形的性质求解即可.
解答 解:如图所示:在AB上取点C′,使AC′=AC,过点C′作C′F⊥AC,垂足为F,交AD与点E.
在Rt△ABC中,依据勾股定理可知BA=10.
∵AC=AC′,∠CAD=∠C′AD,AE=C′E,
∴△AEC≌△AEC′.
∴CE=EC′.
∴CE+EF=C′E+EF.
∴当C′F⊥AC时,CE+EF有最小值.
∵C′F⊥AC,BC⊥AC,
∴C′F∥BC.
∴△AFC′∽△ACB.
∴$\frac{FC′}{BC}$=$\frac{AC′}{AB}$,即$\frac{FC′}{8}$=$\frac{6}{10}$,解得FC′=$\frac{24}{5}$.
故选:C.
点评 本题主要考查的是相似三角形的性质、勾股定理的应用、轴对称图形的性质,熟练掌握相关图形的性质是解题的关键.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | b<c | B. | b=c | C. | b>c | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )| A. | 240米 | B. | 160米 | C. | 150米 | D. | 140米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
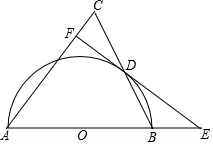 如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.
如图,△ABC是等腰三角形,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线,与AB的延长线交于点E,与AC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②④ | B. | ②③④ | C. | ②④⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解飞行员视力的达标率应使用抽样调查 | |
| B. | 某班7名女生的体重(单位:kg)分别是35,37,38,40,42,42,74,这组数据的众数是74 | |
| C. | 从2000名学生中选200名学生进行抽样调查,样本容量为2000 | |
| D. | 一组数据3,6,6,7,9的中位数是6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com