
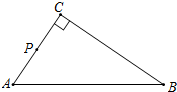
 已知,在Rt△ABC中,∠ACB=90°,P是AC的中点.
已知,在Rt△ABC中,∠ACB=90°,P是AC的中点.分析 先作BC的垂直平分线得到BC的中点0,再以O点为圆心,OB为半径作⊙O交AB于D,连结OD、CD,根据圆周角定理得到∠BDC=90°,接着根据斜边上的中线性质得PC=PD,则∠3=∠4,加上∠1=∠2,于是∠2+∠4=∠1+∠3=90°,则OC⊥PC,然后根据切线的判定定理即可得到PD是⊙O的切线.
解答 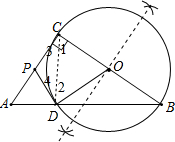 证明:如图,连结OD、CD,
证明:如图,连结OD、CD,
∵BC为直径,
∴∠BDC=90°,
∵P点为Rt△ADC斜边上的中线,
∴PC=PD,
∴∠3=∠4,
∵OC=OD,
∴∠1=∠2,
∴∠2+∠4=∠1+∠3=90°,
∴OC⊥PC,
∴PD是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了尺规作图.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
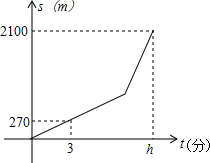 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 26 | B. | 37 | C. | 38 | D. | 51 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com