【题目】如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，BD=CE.
（1）求证：△DEF是等腰三角形；
（2）当∠A=50°时，求∠DEF的度数.
【答案】(1)证明见解析；（2）65°
【解析】试题分析：⑴由AB=AC，可知∠B=∠ C，根据题意易得△ BDE ≌ △ CEF（SAS），从而得到DE=EF，命题得证.
⑵因为∠ A=50°，所以∠ B=∠ C=65°，由⑴可知，∠BDE=∠CEF，所以∠DEB+∠CEF=
∠DEB+∠ BDE=115°，从而∠ DEF=180°-115°=65°.
试题解析：⑴∵ AB=AC，∴ ∠B=∠ C.
在△ BDE和△ CEF中，
，
∴ △ BDE ≌ △ CEF（SAS），则DE=EF，故△ DEF是等腰三角形.
⑵在△ABC中，∵∠A=50°，∴∠B=∠C=65°.
∵ △ BDE ≌ △ CEF，∴ ∠BDE=∠CEF，
∴ ∠DEB+∠CEF=∠DEB+∠ BDE=180°-65°=115°，
则 ∠ DEF=180°-（∠DEB+∠CEF）=180°-115°=65°.
点睛新教材全能解读系列答案
小学教材完全解读系列答案科目：初中数学 来源： 题型：
【题目】如图，点A是线段DE上一点，∠BAC=90°，AB=AC，BD⊥DE，CE⊥DE．
（1）求证：DE=BD+CE．
（2）如果是如图2这个图形，BD、CE、DE有什么数量关系？并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
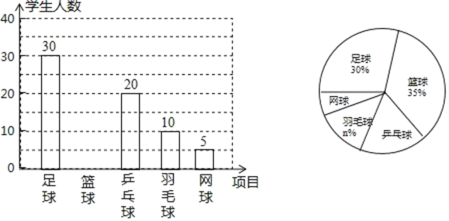
【题目】深圳高级中学(集团)开展“阳光体育活动”，共开设足球，蓝球，乒乓球，羽毛球，网球五项活动，为了了解学生对这五项活动的喜爱情况，随机调查了m名学生(每名学生必须且只能选择这五项运动中的一种)，并根据调查的结果绘制了如图所示不完整的统计图．根据以上统计图提供的信息，解答下列问题：
（1）m= ，n= ；
（2）补全条形统计图；
（3）若深高(集团)共有学生6000人，则喜欢乒乓球的约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，E是线段CD上的点，将△ADE沿AE对折得到△AFE，直线EF交边BC于点G，连接AG.
(1)求证：△ABG≌△AFG；
(2)当DE是CD的一半时，求∠EAG的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，△ABC是正三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB、AC边于M、N两点，连接MN．
探究：在下面两种条件下，线段BM、MN、NC之间的关系，并加以证明．
①AN=NC（如图②）； ②DM//AC（如图③）．
思考：若点M、N分别是射线AB、CA上的点，其它条件不变，再探线段BM、MN、NC之间的关系，在图④中画出图形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小英与她的父亲，母亲计划外出旅游，初步选择了延安、西安、汉中、安康四个城市，由于时间仓促，他们只能去其中一个城市，到底去哪一个城市三人意见不统一，在这种情况下，小英父亲建议，用小英学过的摸球游戏来决定，规则如下：
①在一个不透明的袋子中装一个红球（延安）、一个白球（西安）、一个黄球（汉中）和一个黑球（安康），这四个球除颜色的不同外，其余完全相同；
②小英父亲先将袋中球摇匀，让小英从袋中随机摸出一球，父亲记录下其颜色，并将这个球放回袋中摇匀；然后让小英母亲从袋中随机摸出一球，父亲记录下它的颜色；
③若两人所摸出球的颜色相同，则去该球所表示的城市旅游。否则，前面的记录作废，按规则②重新摸球，直到两人所摸出的球的颜色相同为止。
按照上面的规则，请你解答下列问题：
（1）已知小英的理想旅游城市是西安，小英和母亲随机各摸球一次，均摸出白球的概率是多少？
（2）已知小英母亲的理想旅游城市是汉中，小英和母亲随机各摸球一次，至少有一人摸出黄球的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点。
（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）。
①作∠DAC的平分线AM。②连接BE并延长交AM于点F。
（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小王上周五在股市以收盘价每股
元买进某公司的股票
股，在接下来的一周交易日内，他记下该股票每日收盘价比前一天的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
（1）星期二收盘时，该股票每股多少元?
（2）本周内，该股票收盘时的最高价、最低价分别是多少?
（3）已知买入股票与卖出股票均需支付成交金额的
的交易费，若小王在本周五以收盘价将全部股票卖出，他的收益情况如何?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
