
ЎҫМвДҝЎҝИзНјўЩЈ¬ФЪіӨ·ҪРОABCDЦРЈ¬ABЈҪ12 cmЈ¬BCЈҪ6 cm.өгPСШABұЯҙУөгAҝӘКјПтөгBТФ2 cm/sөДЛЩ¶ИТЖ¶ҜЈ»өгQСШDAұЯҙУөгDҝӘКјПтөгAТФ1 cm/sөДЛЩ¶ИТЖ¶ҜЈ®
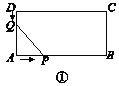
ЙиөгPЈ¬QН¬Кұіц·ўЈ¬УГt(s)ұнКҫТЖ¶ҜөДКұјдЈ®
ЈЁ·ўПЦЈ© DQЈҪ________cmЈ¬APЈҪ________cm.(УГә¬tөДҙъКэКҪұнКҫ)
ЈЁНШХ№Ј©(1)ИзНјўЩЈ¬өұtЈҪ________sКұЈ¬ПЯ¶ОAQУлПЯ¶ОAPПаөИЈҝ
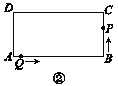
(2)ИзНјўЪЈ¬өгPЈ¬Q·ЦұрөҪҙпBЈ¬AәујМРшФЛ¶ҜЈ¬өгPөҪҙпөгCәу¶јНЈЦ№ФЛ¶ҜЈ®
өұtОӘәОЦөКұЈ¬AQЈҪ![]() CP?
CP?
ЈЁМҪҫҝЈ©ИфөгPЈ¬Q·ЦұрөҪҙпөгBЈ¬AәујМРшСШЧЕAЎӘBЎӘCЎӘDЎӘAөД·ҪПтФЛ¶ҜЈ¬өұөгPУлөгQөЪТ»ҙОПаУцКұЈ¬ЗлЦұҪУРҙіцПаУцөгөДО»ЦГЈ®
Ўҫҙр°ёЎҝt 2t 2
ЎҫҪвОцЎҝ
Ўҫ·ўПЦЎҝЈәёщҫЭВ·іМ=ЛЩ¶ИЎБКұјд,ҝЙөГDQЎўAPөДіӨ¶И;
ЎҫНШХ№ЎҝЈЁ1Ј©өұtГлКұ,DQ=tAQ6-t,AP=2t,УЙ6-t=2tҪЁБў·ҪіМЗуіцЖдҪвјҙҝЙ;
(2)өұQФЪABұЯЙПКұЈ¬AQЈҪ(tЈӯ6)cmЈ¬CPЈҪ(18Јӯ2t)cmЈ¬,УЙAQөДіӨөИУЪПЯ¶ОCPөДіӨөДТ»°лҪЁБў·ҪіМЗуіцЖдҪвјҙҝЙ;
ЎҫМҪҫҝЎҝЈәЙиtГләуөЪТ»ҙОПаУцЈ¬ёщҫЭМвТвҝЙБР·ҪіМ2t-t=30Ј¬ЗуіцКұјдtЈ¬ёщҫЭКұјдЗуПаУцөгөДО»ЦГ.
Ўҫ·ўПЦЎҝ tЈ¬2tЈ»
ЎҫНШХ№Ўҝ(1)2Ј»
(2)УЙМвТвЈ¬өГ AQЈҪ(tЈӯ6)cmЈ¬CPЈҪ(18Јӯ2t)cmЈ¬
ЛщТФtЈӯ6ЈҪ![]() (18Јӯ2t)Ј¬ҪвөГtЈҪ7.5.
(18Јӯ2t)Ј¬ҪвөГtЈҪ7.5.
јҙөұtЈҪ7.5 sКұЈ¬AQЈҪ![]() CP.
CP.
ЎҫМҪҫҝЎҝФЪПЯ¶ОCDөДЦРөгҙҰЈ®


 ұёХҪЦРҝјә®јЩПөБРҙр°ё
ұёХҪЦРҝјә®јЩПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЛДұЯРОOABCЛДёц¶ҘөгөДЧшұк·ЦұрОӘOЈЁ0Ј¬0Ј©Ј¬AЈЁ©Ғ3Ј¬0Ј©Ј¬BЈЁ©Ғ4Ј¬2Ј©Ј¬CЈЁ©Ғ1Ј¬2Ј©Ј®Ҫ«ЛДұЯРОOABCИЖөгOЛіКұХлРэЧӘ90ЎгәуЈ¬өгAЈ¬BЈ¬C·ЦұрВдФЪөгAЎдЈ¬BЎдЈ¬CЎдҙҰЈ® 
ЈЁ1Ј©ЗлДгФЪЛщёшөДЦұҪЗЧшұкПөЦР»ӯіцРэЧӘәуөДЛДұЯРОOAЎдBЎдCЎдЈ»
ЈЁ2Ј©өгCРэЧӘөҪөгCЎдЛщҫӯ№эөД»ЎөД°лҫ¶КЗ Ј¬ өгCҫӯ№эөДВ·ПЯіӨКЗ Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј1Ј¬ТСЦӘөгAЈЁ©Ғ1Ј¬0Ј©Ј¬өгBЈЁ0Ј¬©Ғ2Ј©Ј¬ADУлyЦбҪ»УЪөгEЈ¬ЗТEОӘADөДЦРөгЈ¬Л«ЗъПЯy=![]() ҫӯ№эCЈ¬DБҪөгЗТDЈЁaЈ¬4Ј©ЎўCЈЁ2Ј¬bЈ©Ј®
ҫӯ№эCЈ¬DБҪөгЗТDЈЁaЈ¬4Ј©ЎўCЈЁ2Ј¬bЈ©Ј®
ЈЁ1Ј©ЗуaЎўbЎўkөДЦөЈ»
ЈЁ2Ј©ИзНј2Ј¬ПЯ¶ОCDДЬНЁ№эРэЧӘТ»¶ЁҪЗ¶ИәуөгCЎўDөД¶ФУҰөгCЎдЎўDЎд»№ДЬВдФЪy=![]() өДНјПуЙПВрЈҝИз№ыДЬЈ¬РҙіцДгКЗИзәОРэЧӘөДЈ¬Из№ыІ»ДЬЈ¬ЗлЛөГчАнУЙЈ»
өДНјПуЙПВрЈҝИз№ыДЬЈ¬РҙіцДгКЗИзәОРэЧӘөДЈ¬Из№ыІ»ДЬЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©ИзНј3Ј¬өгPФЪЛ«ЗъПЯy=![]() ЙПЈ¬өгQФЪyЦбЙПЈ¬ИфТФAЎўBЎўPЎўQОӘ¶ҘөгөДЛДұЯРООӘЖҪРРЛДұЯРОЈ¬КФЗуВъЧгТӘЗуөДЛщУРөгPЎўQөДЧшұкЈ®
ЙПЈ¬өгQФЪyЦбЙПЈ¬ИфТФAЎўBЎўPЎўQОӘ¶ҘөгөДЛДұЯРООӘЖҪРРЛДұЯРОЈ¬КФЗуВъЧгТӘЗуөДЛщУРөгPЎўQөДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪРРЛДұЯРОABCDЦРЈ¬![]() өДЖҪРРПЯ
өДЖҪРРПЯ![]() Ҫ»
Ҫ»![]() өДСУіӨПЯУЪөг
өДСУіӨПЯУЪөг![]() Ј¬Ҫ»
Ј¬Ҫ»![]() өДСУіӨПЯУЪөг
өДСУіӨПЯУЪөг![]() Ј¬Ҫ»
Ј¬Ҫ»![]() УЪөг
УЪөг![]() .
.
(1)ЗлЦёіцНјЦРЖҪРРЛДұЯРОөДёцКэЈ¬ІўЛөГчАнУЙ;
(2)![]() Ул
Ул![]() ПаөИВр?ОӘКІГҙ?
ПаөИВр?ОӘКІГҙ?

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПЦУРјЧЎўТТЎўұыөИ¶ајТКіЖ·№«ЛҫФЪДіКРҝӘЙиө°ёвөкЈ¬ёГКРө°ёвөкКэБҝөДЙИРОНіјЖНјИзНјЛщКҫЈ¬ЖдЦРНіјЖНјЦРГ»УРұкЧўПаУҰ№«ЛҫКэБҝөД°Щ·ЦұИЈ®ТСЦӘТТ№«ЛҫҫӯУӘ150јТө°ёвөкЈ¬ЗлёщҫЭёГНіјЖНј»ШҙрПВБРОКМвЈә
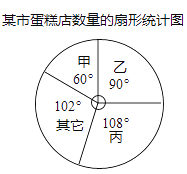
ЈЁ1Ј©ЗујЧ№«ЛҫҫӯУӘөДө°ёвөкКэБҝәНёГКРө°ёвөкөДЧЬКэЈ»
ЈЁ2Ј©јЧ№«ЛҫОӘБЛА©ҙуКРіЎХјУРВКЈ¬ҫц¶ЁФЪёГКРФцЙиө°ёвөкКэБҝҙпөҪИ«КРөД20%Ј¬ЗујЧ№«ЛҫРиТӘФцЙиөДө°ёвөкКэБҝЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЈә![]() Ј¬OBЈ¬OMЈ¬ONКЗ
Ј¬OBЈ¬OMЈ¬ONКЗ![]() ДЪөДЙдПЯЈ®
ДЪөДЙдПЯЈ®
![]() ИзНј1Ј¬ИфOMЖҪ·Ц
ИзНј1Ј¬ИфOMЖҪ·Ц![]() Ј¬ONЖҪ·Ц
Ј¬ONЖҪ·Ц![]() өұЙдПЯOBИЖөгOФЪ
өұЙдПЯOBИЖөгOФЪ![]() ДЪРэЧӘКұЈ¬
ДЪРэЧӘКұЈ¬![]() ______¶И
______¶И![]()
![]() ТІКЗ
ТІКЗ![]() ДЪөДЙдПЯЈ¬ИзНј2Ј¬Иф
ДЪөДЙдПЯЈ¬ИзНј2Ј¬Иф![]() Ј¬OMЖҪ·Ц
Ј¬OMЖҪ·Ц![]() Ј¬ONЖҪ·Ц
Ј¬ONЖҪ·Ц![]() Ј¬өұ
Ј¬өұ![]() ИЖөгOФЪ
ИЖөгOФЪ![]() ДЪРэЧӘКұЈ¬Зу
ДЪРэЧӘКұЈ¬Зу![]() өДҙуРЎЈ®
өДҙуРЎЈ®
![]() ФЪ
ФЪ![]() өДМхјюПВЈ¬Иф
өДМхјюПВЈ¬Иф![]() Ј¬өұ
Ј¬өұ![]() ФЪ
ФЪ![]() ИЖOөгТФГҝГл
ИЖOөгТФГҝГл![]() өДЛЩ¶ИДжКұХлРэЧӘtГлЈ¬ИзНј3Ј¬Иф
өДЛЩ¶ИДжКұХлРэЧӘtГлЈ¬ИзНј3Ј¬Иф![]() Јә
Јә![]() Јә3Ј¬ЗуtөДЦөЈ®
Јә3Ј¬ЗуtөДЦөЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪсДкК®Т»»ЖҪрЦЬЖЪјдЈ¬ҫЕХҜ№ө7МмЦРГҝМмВГУОИЛКэөДұд»ҜЗйҝцИзПВұнЈЁХэКэұнКҫұИ9ФВ30ИХ¶аөДИЛКэЈ¬ёәКэұнКҫұИ9ФВ30ИХЙЩөДИЛКэЈ©Јә
ИХЖЪ | 1ИХ | 2ИХ | 3ИХ | 4ИХ | 5ИХ | 6ИХ | 7ИХ |
ИЛКэұд»Ҝ/НтИЛ | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)ЎўЗлЕР¶П7МмДЪУОҝНИЛКэБҝЧо¶аәНЧоЙЩөДёчКЗДДТ»МмЈҝЛьГЗПаІо¶аЙЩНтИЛЈҝЈЁ5·ЦЈ©
(2)ЎўИз№ы9ФВ30ИХВГУОИЛКэОӘ2.5НтИЛЈ¬ЖҪҫщГҝИЛПы·С500ФӘЈ¬ЗлОК·зҫ°ЗшФЪҙЛ7МмДЪЧЬКХИлОӘ¶аЙЩНтФӘЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЎчABCКЗөИұЯИэҪЗРОЈ¬ТФABОӘЦұҫ¶ЧчЎСOЈ¬Ҫ»BCұЯУЪөгDЈ¬Ҫ»ACұЯУЪөгFЈ¬ЧчDEЎНACУЪөгEЈ® 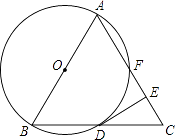
ЈЁ1Ј©ЗуЦӨЈәDEКЗЎСOөДЗРПЯЈ»
ЈЁ2Ј©ИфЎчABCөДұЯіӨОӘ4Ј¬ЗуEFөДіӨ¶ИЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ°СПВБРёчКэМоФЪПаУҰөДҙуАЁәЕЦРЈә8Ј¬©Ғ![]() Ј¬+2.8Ј¬ҰРЈ¬
Ј¬+2.8Ј¬ҰРЈ¬![]() Ј¬©Ғ0.003Ј¬0Ј¬©Ғ100Ј¬©Ғ3.626626662ЎӯЎӯ
Ј¬©Ғ0.003Ј¬0Ј¬©Ғ100Ј¬©Ғ3.626626662ЎӯЎӯ
ХэКэјҜәП{_____ЎЎЎӯ}
ХыКэјҜәП{_____Ўӯ}
ёә·ЦКэјҜәП{_____ЎЎЎӯ}
ОЮАнКэјҜәП{_____ЎЎЎӯ}Ј®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com