
【题目】(1)若|x+5|=2,则x= ;
(2)代数式|x﹣1|+|x+3|的最小值为 ,当取此最小值时,x的取值范围是 ;
(3)解方程:|2x+4|﹣|x﹣3|=9.
【答案】(1)﹣3或﹣7;(2)4,﹣3≤x≤1;(3)x=﹣16或x=![]() .
.
【解析】试题分析:(1)解绝对值方程.
(2)数形结合,利用绝对值的意义在数轴上求最小值.
(3)分类讨论,化简绝对值,解绝对值方程.
【解答】试题分析:
试题解析:
解:(1)∵|x+5|=2,
∴x+5=2或x+5=﹣2,
解得:x=﹣3或x=﹣7.
(2)由数形结合得,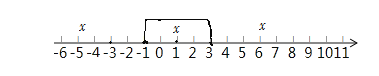
代数式|x﹣1|+|x+3|的最小值为1﹣(﹣3)=4,当取此最小值时,x的取值范围是﹣3≤x≤1.
(3)当x≤﹣2时,原方程可化为:﹣2x﹣4+x﹣3=9,
解得:x=﹣16,
当x≥3时,原方程可化为:2x+4﹣x+3=9,
解得:x=2
与x≥3不符;
当﹣2<x<3时,原方程可化为:2x+4+x﹣3=9,
解得:x=![]() .
.
综上所述,方程的解为:x=﹣16或x=![]() .
.
故答案为:﹣3或﹣7;4,﹣3≤x≤1.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】一次数学课上,老师在黑板上画了如图图形,并写下了四个等式:
①BD=CA,②AB=DC,③∠B=∠C,④∠BAE=∠CDE.
要求同学从这四个等式中选出两个作为条件,推出AE=DE.请你试着完成老师提出的要求,并说明理由.(写出一种即可)
已知:____(请填写序号),求证:AE=DE.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种出租车的收费标准是:起步价7元(即行驶距离不超过3km都需付7元车费);超过3km以后,每增加1km,加收2.4元(不足1km按1km计),某人乘出租车从甲地到乙地共支付车费19元,则此人从甲地到乙地经过的路程( ).
A. 正好8km B. 最多8km
C. 至少8km D. 正好7km
查看答案和解析>>
科目:初中数学 来源: 题型:
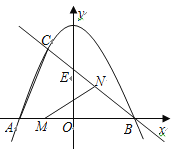
【题目】如图,抛物线![]() 与x轴交于点A、点B,与直线
与x轴交于点A、点B,与直线![]() 相交于点B、点C,直线
相交于点B、点C,直线![]() 与y轴交于点E。
与y轴交于点E。
(1)写出直线BC的解析式。
(2)求△ABC的面积。
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A,B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积S与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,E、F分别是平行四边形ABCD的AD、BC边上的点,且AE=CF。
(1)求证:△ABE≌△CDF。
(2)若M、N分别是BE、DF的中点,连结MF、EN,
求证:四边形MFNE是平行四边形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com