
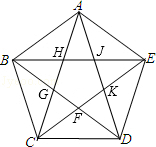
 如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$.
如图,向正五边形ABCDE区域内均匀掷点,落在五边形FGHJK区域内的概率为$\frac{7-3\sqrt{5}}{2}$. 分析 先判断出五边形HGFKJ是正五边形,进而得出正五边形HGFKJ∽正五边形ACBDE,再用△HAB∽△ABE得出两个五边形的边长的关系即可.
解答 解:正五边形ABCDE,
∴∠BAE=∠ABC=BCD=∠CDE∠AED=108°,AB=BC=CD=DE=AE,
∴△ABC≌△ABE,
∴AC=BE,同理:△ABH≌△△BCG≌△AJE,
∴AH=CG=JE,
∴HJ=HG,
同理:FG=FK=JK=HG,
∴五边形HGFKJ是正五边形,
∴正五边形HGFKJ∽正五边形ACBDE,
设HE=CD=a,HJ=x,
由题意,△HAB∽△ABE,
∴$\frac{a-x}{x}=\frac{a}{2a-x}$,
∴x=$\frac{3-\sqrt{5}}{2}x$
∴落在五边形FGHJK区域内的概率为 $\frac{{S}_{HGFKJ}}{{S}_{ABCDE}}=(\frac{3-\sqrt{5}}{2})^{2}$=$\frac{7-3\sqrt{5}}{2}$,
故答案为$\frac{7-3\sqrt{5}}{2}$.
点评 此题考查了几何概率的求法,利用面积比计算出几何概率,即相似三角形的判定和性质,根据题意找出五边形的面积比是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
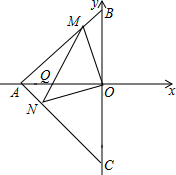 已知A(-4,0),B(0,4),C(0,-4),过O作OM⊥ON交AB、AC于M、N两点
已知A(-4,0),B(0,4),C(0,-4),过O作OM⊥ON交AB、AC于M、N两点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
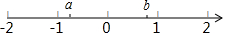 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com