
(本题满分12分)
【问题背景】
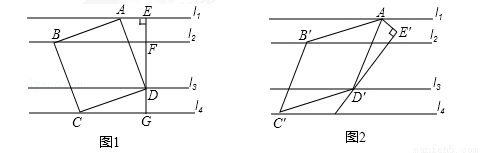
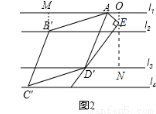
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
【问题探究】
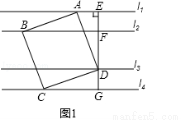
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为_ _.
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.
(1)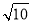 ;(2)
;(2)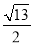 或
或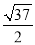 ;(3)
;(3)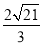 .
.
【解析】
试题分析:(1)证明∴△AED≌△DGC,得出CG=ED=3,AE=DG=1,由勾股定理得到正方形的边长AD;
(2)过B作BE⊥l1于点E,反向延长BE交l4于点F,则BE=1,BF=3,可以证明△AEB∽△BFC,分AB是较短的边和AB是长边两种情况讨论;
(3)过点E作ON垂直于l1分别交l1,l3于点O,N,由题意得∠OAE=30°,则∠ED′N=60°,由图1知,△AED≌△DGC,得到AE=DG=1,进一步得到EO,EN,ED′的长,由勾股定理可求出菱形的边长.
试题解析:(1)∵ABCD是正方形,∴AD=CD,∠ADC=90°,∴∠ADE+∠CDG=90°,∵∠AED=90°,∴∠EAD+∠ADE=90°,∴∠EAD=∠CDG,∵∠AED=∠DGC=90°,∴△AED≌△DGC,∴CG=ED=3,AE=DG=1,∴AD=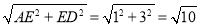 ,∴正方形的边长是
,∴正方形的边长是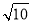 ;
;
(2)过B作BE⊥l1于点E,反向延长BE交l4于点F,则BE=1,BF=3,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠ABE+∠FBC=90°,又∵直角△ABE中,∠ABE+∠EAB=90°,∴∠FBC=∠EAB,∴△AEB∽△BFC,当AB是较短的边时,如图(a),AB=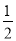 BC,则AE=
BC,则AE=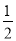 BF=
BF=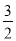 ,在直角△ABE中,AB=
,在直角△ABE中,AB=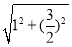 =
=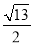 ;
;
当AB是长边时,如图(b),同理可得:BC=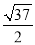 ;故答案为:
;故答案为: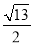 或
或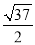 ;
;

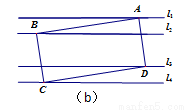
(3)过点E作ON垂直于l1分别交l1,l3于点O,N,由题意得∠OAE=30°,则∠ED′N=60°,由图1知,△AED≌△DGC,∴AE=DG=1,故EO=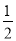 ,EN=
,EN=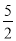 ,ED′=
,ED′=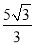 ,由勾股定理可知菱形的边长为:
,由勾股定理可知菱形的边长为: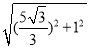 =
=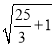 =
=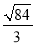 =
=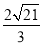 .
.
考点:四边形综合题.


科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:解答题
已知正方形OABC中,O为坐标原点,点A在y轴的正半轴上,点C在x轴的正半轴上,点B(4,4).二次函数y=-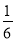 x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
x2+bx+c的图象经过点A、B.点P(t,0)是x轴上一动点,连接AP.
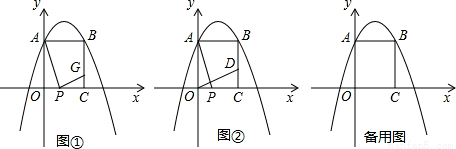
(1)求此二次函数的解析式;
(2)如图①,过点P作AP的垂线与线段BC交于点G,当点P在线段OC(点P不与点C、O重合)上运动至何处时,线段GC的长有最大值,求出这个最大值;
(3)如图②,过点O作AP的垂线与直线BC交于点D,二次函数y=-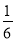 x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
x2+bx+c的图象上是否存在点Q,使得以P、C、Q、D为顶点的四边形是以PC为边的平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:填空题
抛物线y=2x2向左平移1个单位,再向下平移3个单位,得到的抛物线表达式为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:选择题
10名九年级学生的体重分别是41,48,50,53,49,50,53,67,51,53(单位:kg).这组数据的极差是( )
A.26 B.25 C.24 D.12
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:解答题
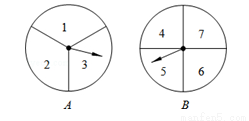
(本题满分8分)甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:填空题
请写出一个开口向上,与y轴交点的纵坐标为2的抛物线的函数表达式 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(-4,0),B(-1,0)两点.
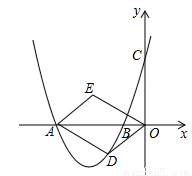
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.如图,若四边形ODAE是以OA为对角线的平行四边形,当平行四边形ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省耒阳市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A.2 B.2
B.2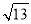 C.2
C.2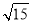 D.8
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com