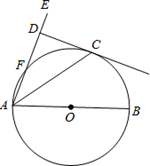
(1)证明:连接OC。
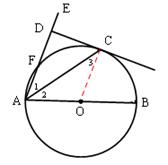
∵CD是⊙O的切线,∴CD⊥OC。
又∵CD⊥AE,∴OC∥AE。∴∠1=∠3。
∵OC=OA,∴∠2=∠3。
∴∠1=∠2,即∠EAC=∠CAB。
(2)解:①连接BC。
∵AB是⊙O的直径,CD⊥AE于点D,
∴∠ACB=∠ADC=90°。
∵∠1=∠2,∴△ACD∽△ABC。∴
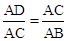
。
∵AC
2=AD
2+CD
2=4
2+8
2=80,
∴AB=
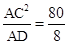
=10。
∴⊙O的半径为10÷2=5。
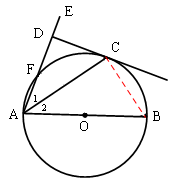
②连接CF与BF。
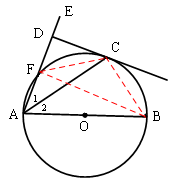
∵四边形ABCF是⊙O的内接四边形,
∴∠ABC+∠AFC=180°。
∵∠DFC+∠AFC=180°,∴∠DFC=∠ABC。
∵∠2+∠ABC=90°, ∠DFC+∠DCF=90°,
∴∠2=∠DCF。
∵∠1=∠2,∴∠1=∠DCF。
∵∠CDF=∠CDF,∴△DCF∽△DAC。∴
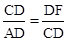
。∴DF=
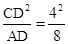
=2。
∴AF=AD-DF=8-2=6。
∵AB是⊙O的直径,∴∠BFA=90°。
∴BF=

=8。∴tan∠BAD=
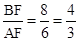
。
(1)连接OC,由CD是⊙O的切线,CD⊥OC,又由CD⊥AE,即可判定OC∥AE,根据平行线的性质与等腰三角形的性质,即可证得∠EAC=∠CAB。
(2)①连接BC,易证得△ACD∽△ABC,根据相似三角形的对应边成比例,即可求得AB的长,
从而可得⊙O的半径长。
②连接CF与BF.由四边形ABCF是⊙O的内接四边形,易证得△DCF∽△DAC,然后根据
相似三角形的对应边成比例,求得AF的长,又由AB是⊙O的直径,即可得∠BFA是直角,利用勾股定理求得BF的长,即可求得tan∠BAE的值。

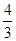


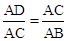 。
。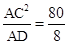 =10。
=10。
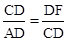 。∴DF=
。∴DF=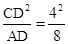 =2。
=2。 =8。∴tan∠BAD=
=8。∴tan∠BAD=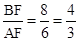 。
。 

 阅读快车系列答案
阅读快车系列答案